Phương pháp giải hình 9 hệ thức góc và cạnh trong tam giác vuông (có đáp án và lời giải chi tiết)

Bài 4-5. MỘT SỐ HỆ THỨC VỀ CẠNH VÀ GÓC TRONG TAM GIÁC VUÔNG
ỨNG DỤNG THỰC TẾ CÁC TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN
A. KIẾN THỨC TRỌNG TÂM
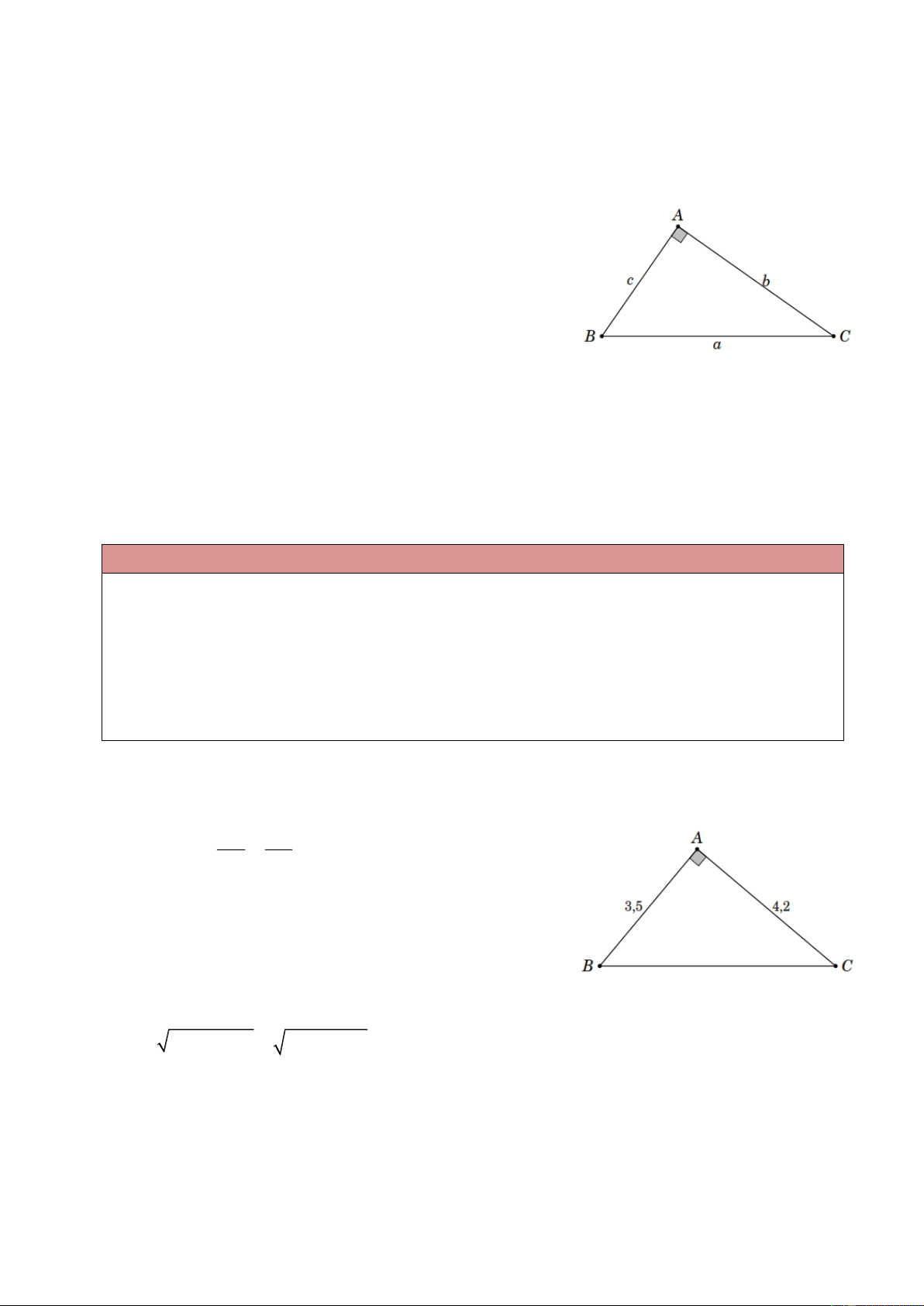
1. Liên hệ giữa cạnh và góc trong tam giác vuông
Trong một tam giác vuông, mỗi cạnh góc vuông bằng
 Tích của cạnh huyền với sin của góc đối hoặc cô-sin của góc kề.
 Tích của cạnh góc vuông kia với tang góc đối hoặc cô-tang góc kề. Trong hình bên, ta có
b  a  sin B  a  cos C;
b  c  tan B  c  cot C;
c  c  sin C  a  cos B;
c  b  tan C  b  cot . B
2. Giải tam giác vuông
 Giải tam giác vuông là tìm tất cả các cạnh và các góc còn lại của tam giác vuông đó khi biết
trước hai cạnh hoặc một cạnh và một góc nhọn.
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1: Giải tam giác vuông
 Vận dụng các công thức liên hệ giữa cạnh và góc trong tam giác vuông để tìm cạnh.
 Vận dụng công thức liên hệ giữa cạnh và đường cao trong tam giác vuông để tìm cạnh.
 Vận dụng các tỉ số lượng giác của góc nhọn để tính góc. Lưu ý:
 Nếu cho trước 1 góc nhọn thì nên tìm góc nhọn còn lại.
 Nếu cho trước hai cạnh thì dùng định lý Py-ta-go tìm cạnh thứ hai.
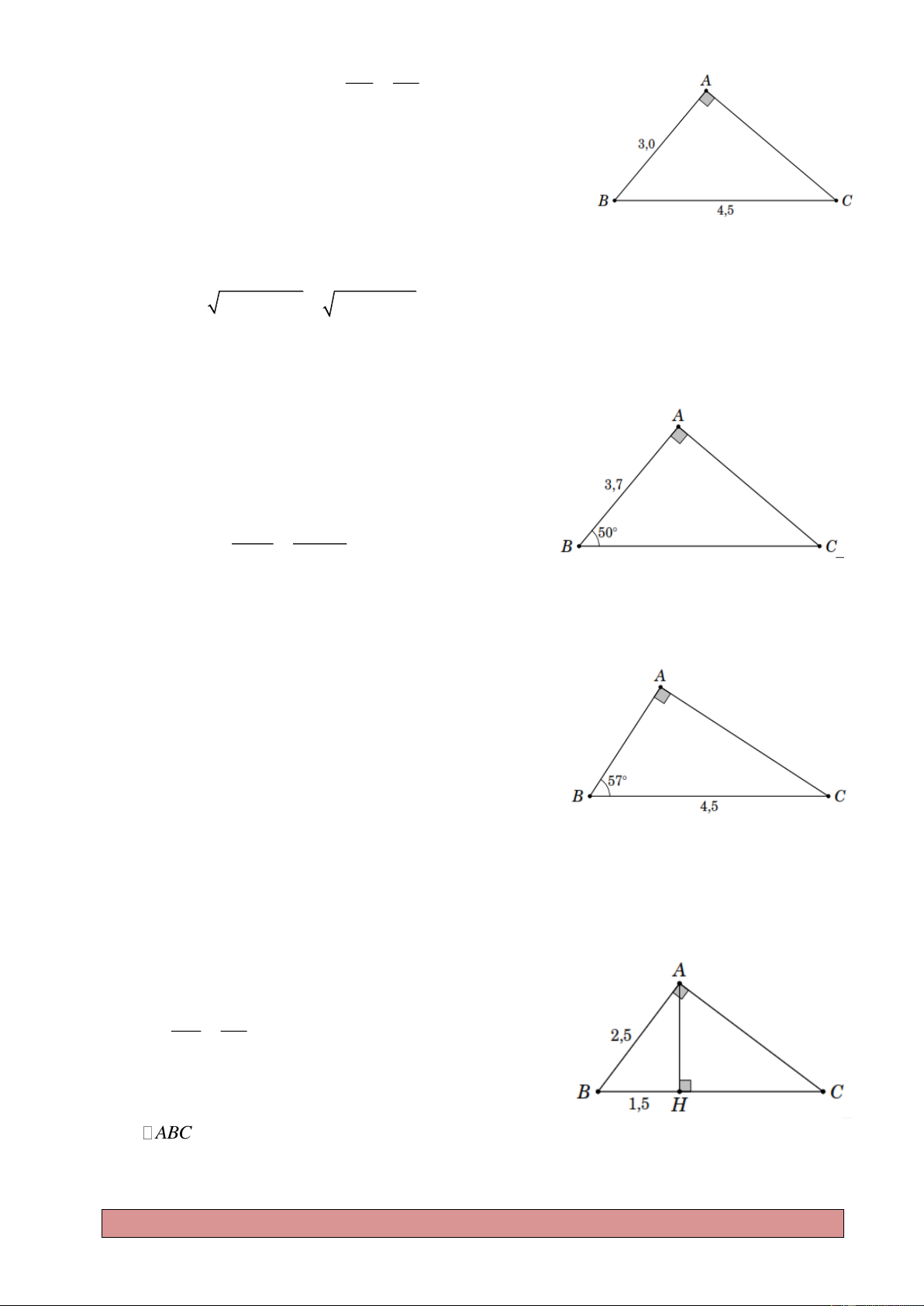
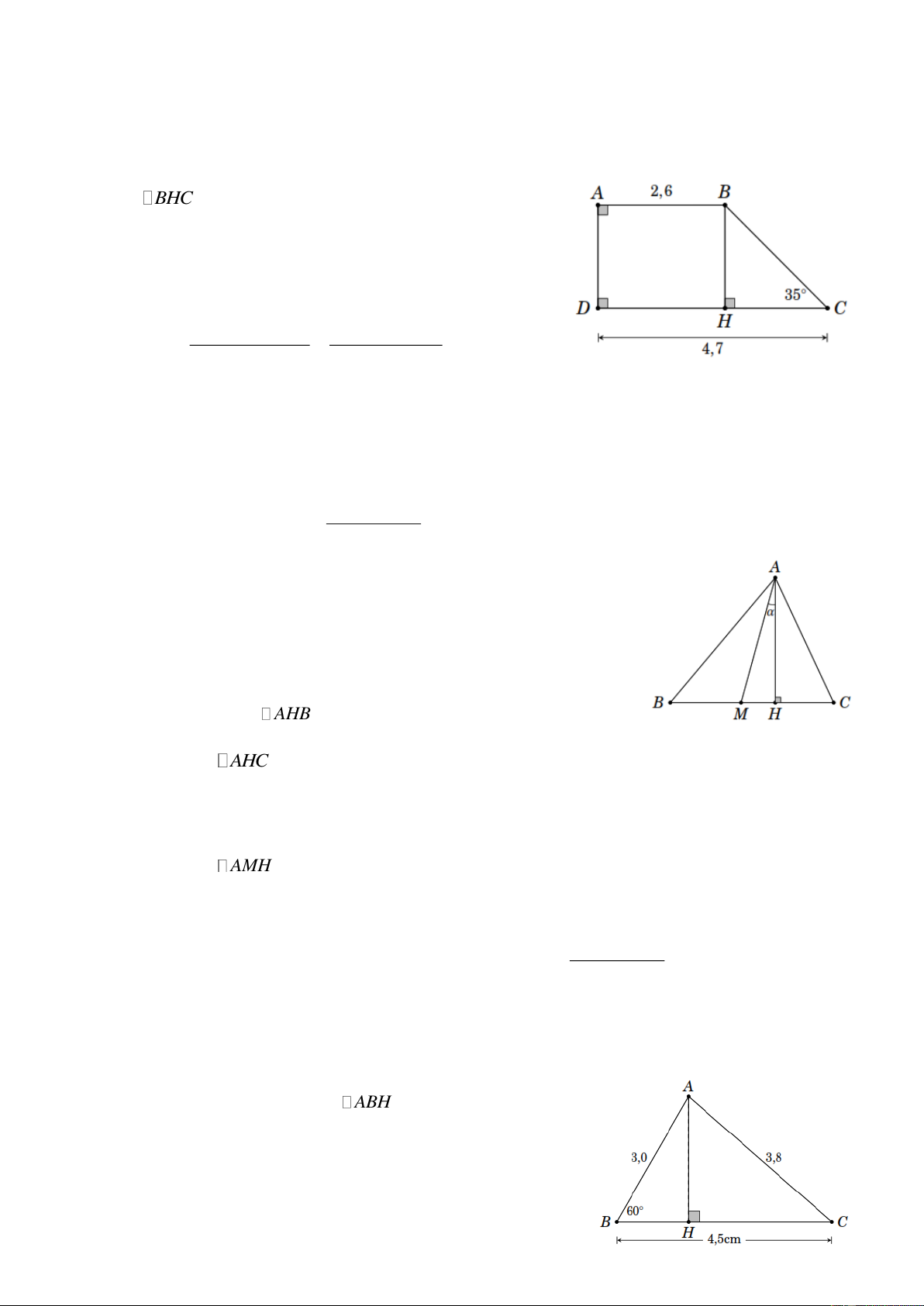
Ví dụ 1. Giải tam giác ABC vuông tại A , biết AB  3, 5 và AC  4, 2 . Lời giải AC 4, 2 Ta có tan B    tan 50 1  2. AB 3, 5 Suy ra ˆ B  50 1  2 mà ˆ ˆ B C 90   nên ˆ  ˆ
C  90  B  90  50 1  2  39  48 .
Mặt khác, theo định lí Py-ta-go ta có 2 2 2 2 BC 
AB  AC  3,5  4, 2  5,5.
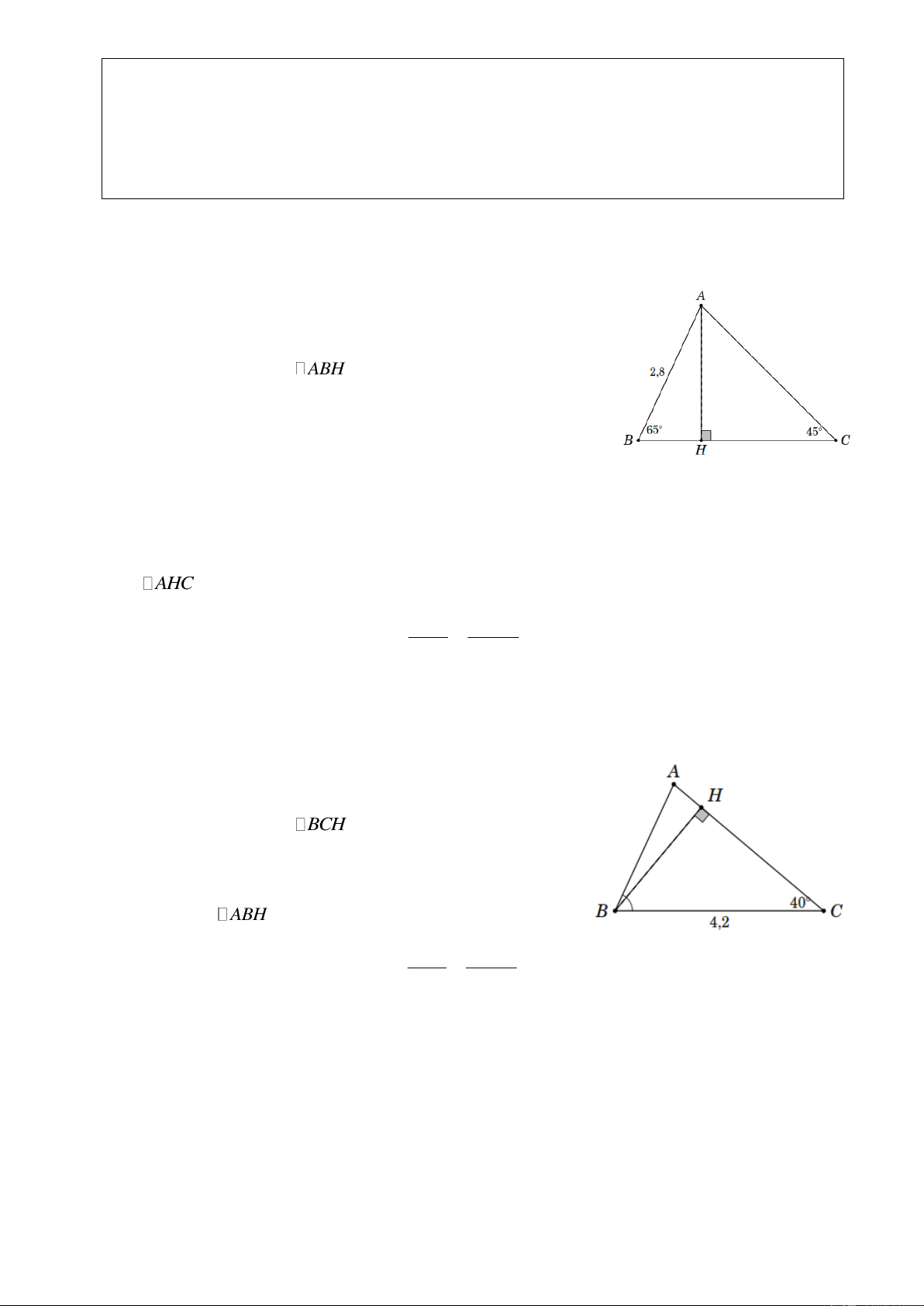
Ví dụ 2. Giải tam giác ABC vuông tại A , biết AB  3, 0 và BC  4,5 . Lời giải Trang 1 AB 3, 0
Do giả thiết ta có sin C    sin 4149 suy ra BC 4,5 ˆ C  4149 . Mà ˆ ˆ B C 90   nên ˆ  ˆ
B  90  C  90  4149  48 1   1 .
Mặt khác theo định lí Py-ta-go 2 2 2 2 2 2
BC  AB  AC  AC  BC  AB . suy ra 2 2 2 2 AC 
BC  AB  4,5  3, 0  3, 4.
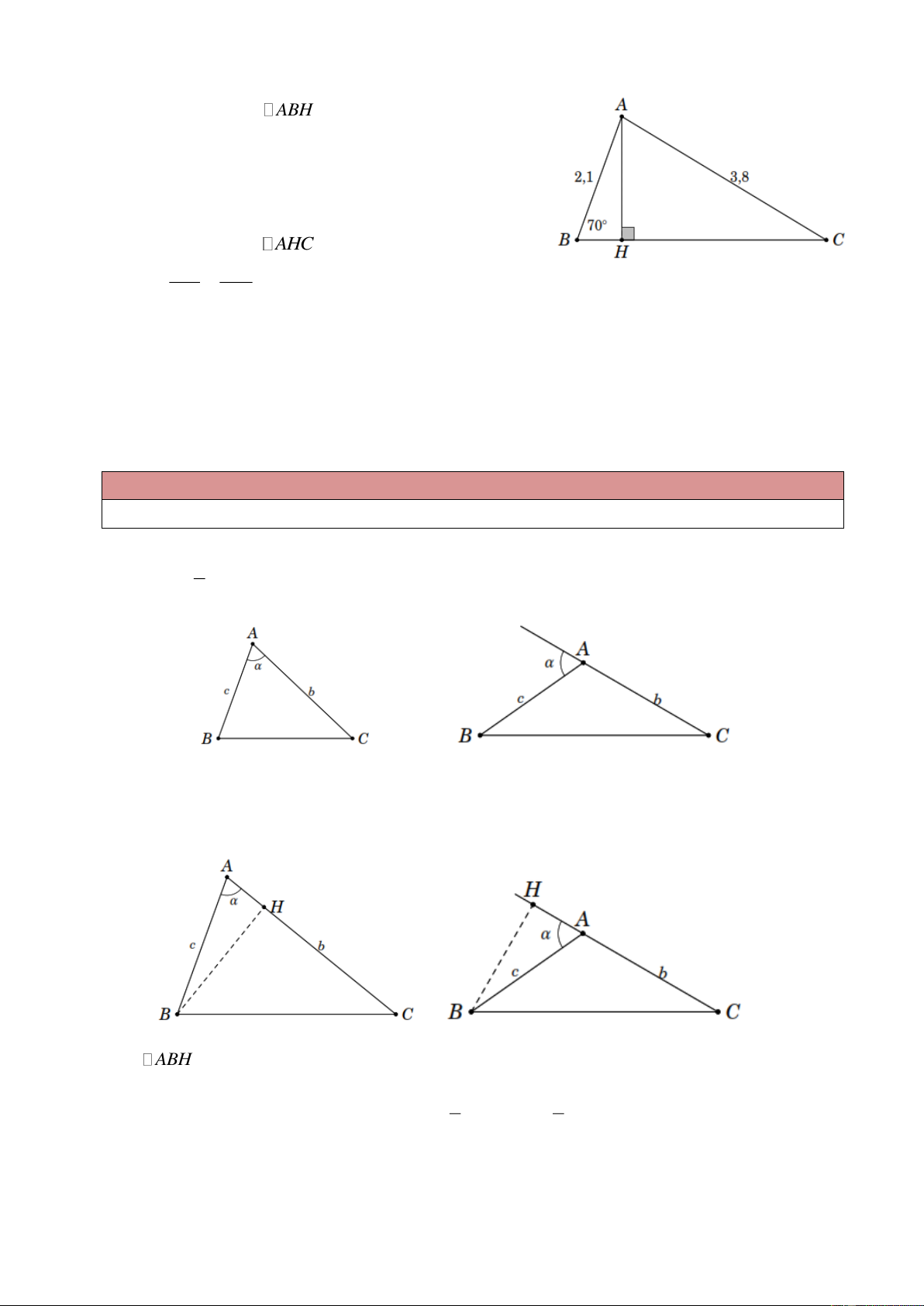
Ví dụ 3. Giải tam giác ABC vuông tại A , biết ˆ B 50  và AB  3, 7 . Lời giải Ta có ˆ  ˆ C 90 B 90 50 40      . Mặt khác AC AB tan B 3, 7 tan 50      4,4 . Tương tự AB 3, 7 BC    5,8 . cos B cos 50
Ví dụ 4. Giải tam giác ABC vuông tại A , biết ˆ B 57  và BC  4, 5 . Lời giải Ta có ˆ C 90 57 33    . Mặt khác AB BC cos B 4,5 cos 57      2,5 và AC BC sin B 4,5 sin 57      3,8.
Ví dụ 5. Cho tam giác ABC vuông tại A , đường cao AH . Biết AB  2, 5 , BH  1, 5 . Tính ˆ B , ˆ C và AC . Lời giải
Xét tam giác ABH vuông tại H , ta có BH 1,5 cos B    cos53 8
  suy ra ˆB  53 8   . AB 2,5 Mà ˆ ˆ B C 90   nên ˆ C  90  53 8   36 5   2.
Xét ABC vuông tại A , ta có
AC  AB  tan B  2,5 tan 53 8    3,3.
Dạng 2: Giải tam giác nhọn Trang 2
 Bước 1: Vẽ đường cao để vận dụng các hệ thức lượng trong tam giác vuông.
 Bước 2: Tính đường cao rồi tính các độ dài cạnh hay góc trong tam giác đã cho.
Lưu ý: Dùng đường cao làm trung gian để tính các độ dài cạnh hoặc số đo góc.
 Nếu tam giác cho trước một cạnh (hoặc một góc) thì khi vẽ đường cao không thể chia đôi
cạnh đó (hoặc góc đó) vì như vậy sẽ khó khăn cho việc tính toán.
Ví dụ 6. Cho tam giác ABC có ˆ B 65  , ˆ C 45 
và AB  2,8cm . Tính các góc và cạnh còn lại của
tam giác đó (gọi là giải tam giác ABC ). Lời giải Ta có ˆ  ˆ ˆ A 180 B C 180 65 45 70        .
Kẻ đường cao AH . Xét ABH vuông tại H , ta có AH AB sin B 2,8 sin 65      2,5  4 cm . Tương tự BH AB cos B 2,8 cos 65     1,1  8 cm .
Mặt khác, do giả thiết suy ra tam giác HAC vuông cân tại H nên HA  HC . Do đó
BC  2,54 1,18  3, 7cm .
Xét AHC vuông tại H , ta có HA 2, 54 AC    3,6  cm. sin C sin 45
Ví dụ 7. Giải tam giác ABC biết ˆ B 65  , ˆ C 40  và BC  4, 2cm . Lời giải Ta có ˆ  ˆ ˆ A 180 B C 180 65 40 75        .
Kẻ đường cao BH . Xét BCH vuông tại H , ta có BH BC sin C 4, 2 sin 40      2,7  0 cm .
Tương tự, xét ABH vuông tại H , ta có BH 2, 70 AB    2,   8 cm. sin A sin 75 Mặt khác, ta có AC
 AH  CH  BH cot A cotC
 2,70cot 75  cot 40   3,  9 cm
Ví dụ 8. Giải tam giác nhọn ABC biết AB  2,1 , AC  3,8 và ˆ B 70  . Trang 3 Lời giải
Vẽ AH  BC . Xét ABH vuông tại H , ta có AH AB sin B 2,1 sin 70     1,97 . Tương tự, xét BH AB cos B 2,1 cos 70      0,72 . Mặt khác, xét AHC vuông tại H , ta có AH 1,97 sin C    sin 311  4 do đó ˆ C  311  4 . AC 3,8 Mà ˆ
A  180  70  311  4   78  46 .
Ta có HC  AC  cos C  3,80  cos 311  4  3,25.
Mà BC  BH  HC  0, 72  3, 25  3, 97 .
Dạng 3: Tính diện tích tam giác, tứ giác
 Tính các yếu tố cần thiết rồi thay vào công thức tính diện tích và thực hiện phép tính.
Ví dụ 9. Cho tam giác ABC như hình vẽ bên. Chứng minh rằng diện tích tam giác ABC có diện 1 tích là S 
b c sin . 2 Lời giải
Vẽ đường cao BH của tam giác ABC .
Xét ABH vuông tại H , ta có BH  ABsin A  c sin . Do đó diệ 1 1
n tích S của tam giác ABC là S 
 AC  BH  bc sin . 2 2
Nhận xét: Qua ví dụ này ta có thêm một cách tính diện tích tam giác. Diện tích tam giác bằng nửa
tích hai cạnh nhân với sin của góc nhọn xen giữa hai đường thẳng chứa hai cạnh đó. Trang 4
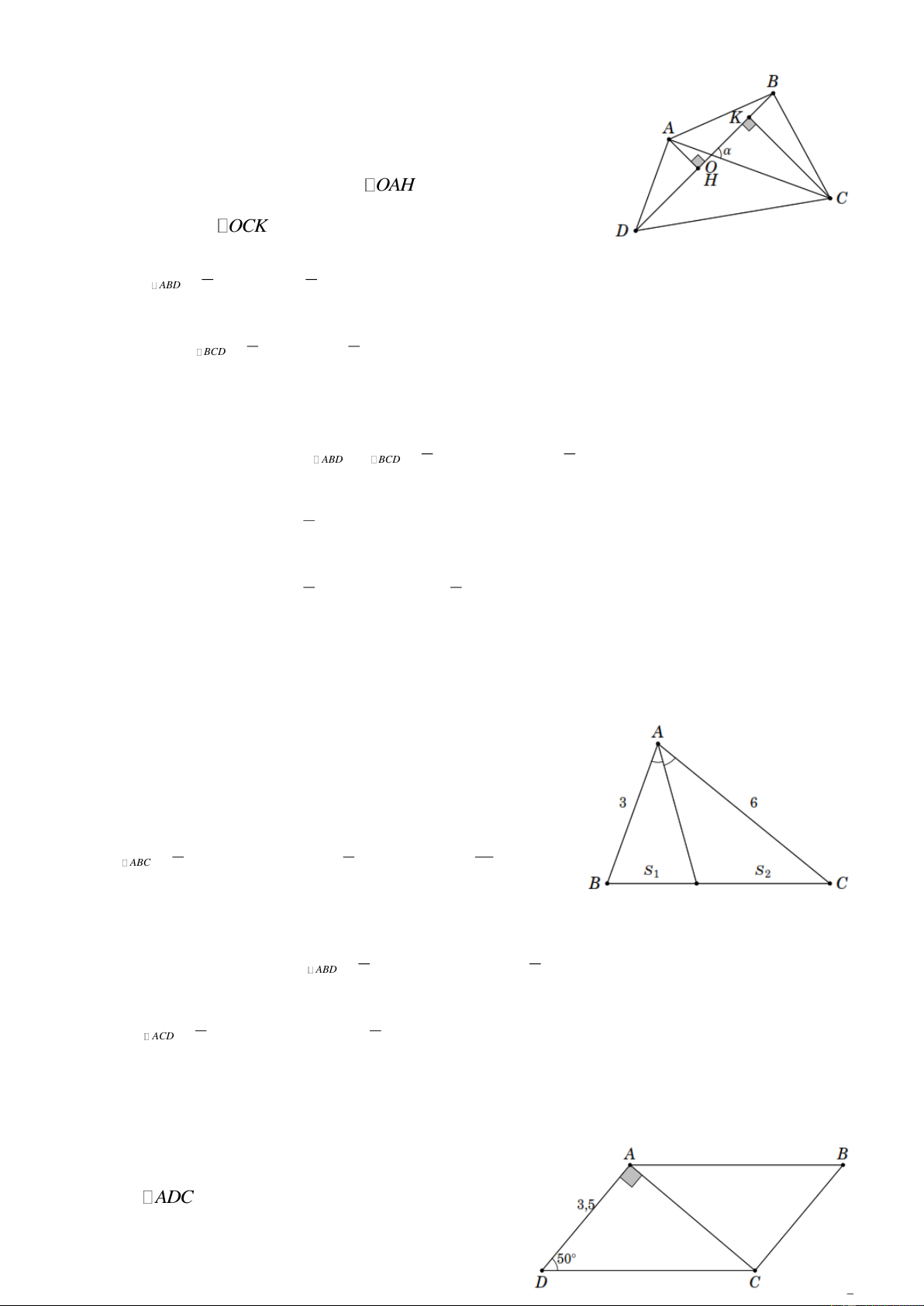
Ví dụ 10. Tứ giác ABCD như hình vẽ phía dưới. Biết AC  3,8 , 
BD  5, 0 và   65 . Tính diện tích của tứ giác đó. Lời giải
Vẽ AH  BD và CK  BD . Xét OAH ta có AH  OAsin .
Tương tự, xét OCK ta có CK  OC sin . 1 1 Mà S
  BD  AH   BD OAsin. ABD 2 2 Tương tự 1 1 S
  BD CK   BD OC sin. BCD 2 2
Gọi S là diện tích tứ giác ABCD ta có 1 1 S  S  S
  BD OAsin   BD OC sin ABD BCD 2 2 1
  BD sin OA OC 2 1 1 BD AC sin  5, 0 3,8 sin 65          8,6 . 2 2
Ví dụ 11. Tam giác ABC có ˆ ˆ B C 60  
, AB  3, AC  6 . Tính độ dài đường phân giác AD . Lời giải    Do giả thiết ˆ ˆ B C 60  
nên BAC  180  60  120 . Mà 
AD là đường phân giác nên BAD  CAD  60 . Mà 1 1  18 S AB AC sin BAC 3 6 sin120 sin 60           . ABC 2 2 2 Mặt khác 1 1 S AB AD sin BAD AB AD sin 60         ABD 2 2 1 1  và S
  AC  AD sin DAC   AC  AD sin 60 ACD 2 2
Ví dụ 12. Hình bình hành ABCD có AC  AD và AD  3,5 , ˆ D 50 
. Tính diện tích của hình bình hành. Lời giải
Xét ADC vuông tại A , ta có Trang 5 AC AD tan ADC 3,5 tan 50     .
Khi đó gọi S là diện tích hình bình hành ABCD, ta có S AD AC 3,5 3,5 tan 50      14,6.
Dạng 4: Ứng dụng thực tế của hệ thức lượng trong tam giác vuông
 Vẽ lại hình vẽ theo yêu cầu bài toán (chú ý tạo ra tam giác vuông).
 Xác định các yếu tố cần thiết rồi tính theo các hệ thức giữa cạnh và góc trong tam giác
hoặc sử dụng tỉ số lượng giác của góc nhọn để tìm góc.
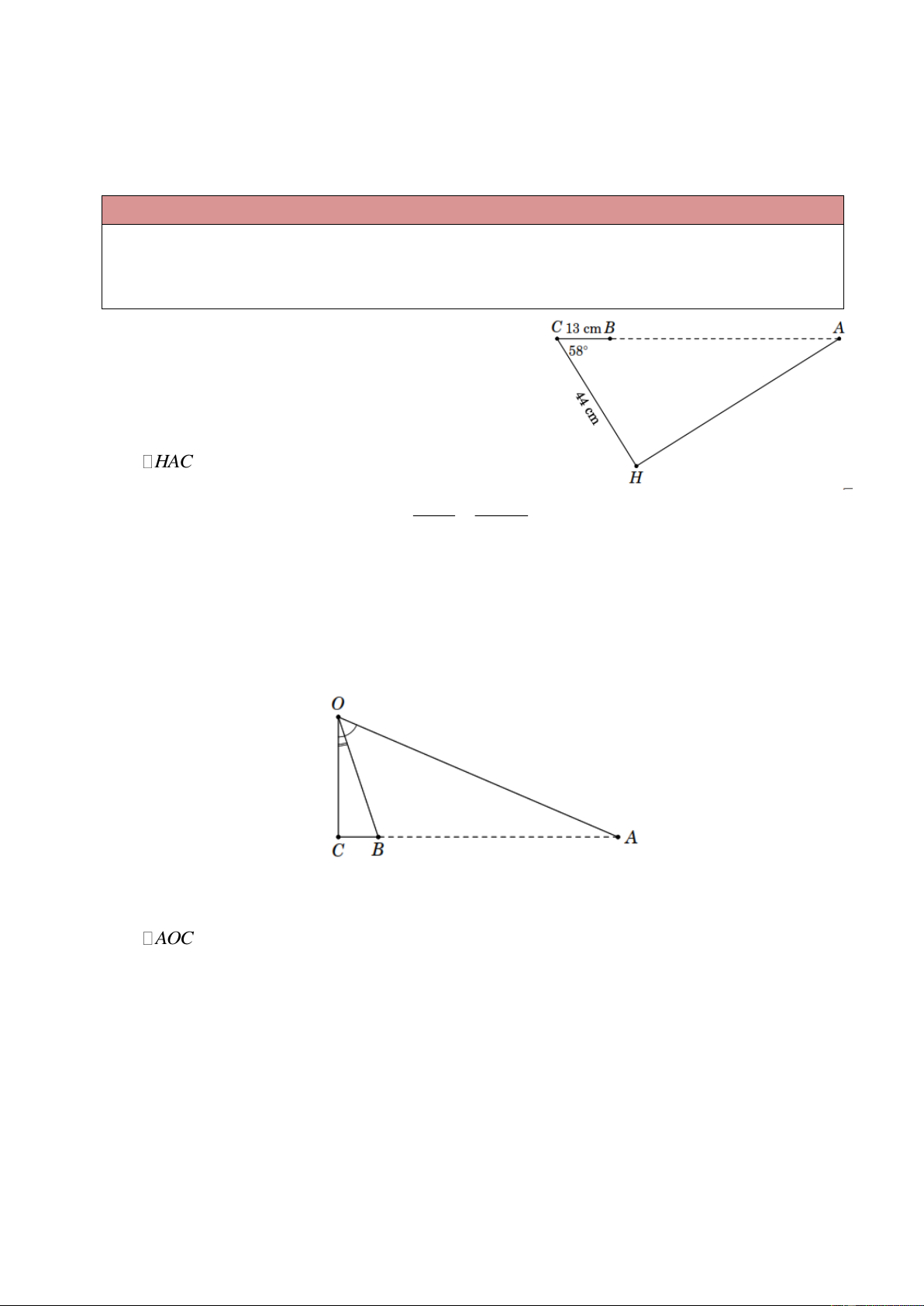
Ví dụ 13. Tính khoảng cách giữa hai điểm A và B trên
một bờ hồ nước sâu, biết ˆ C 58  , CB  13m ,
CH  44m như hình bên. Lời giải
Xét HAC vuông tại H , ta có HC 44 AC      83 m . cos C cos 58
Mà AB  AC  BC  83 13  7  0 m.
Ví dụ 14. Trong hình vẽ bên dưới, tính chiều rộng 
AB của con sông, biết OC  47m , AOC  74 , BOC 23  . Lời giải  
Xét AOC vuông ở C , ta có AC  OC  tan 74 và BC  OC  tan 23 . Do đó AB
 AC  BC  OC  tan 74  OC  tan 23
 OC tan 74  tan 23 
 47 tan 74  tan 23  144,  0 m.
Vậy AB bằng 144, 0m .
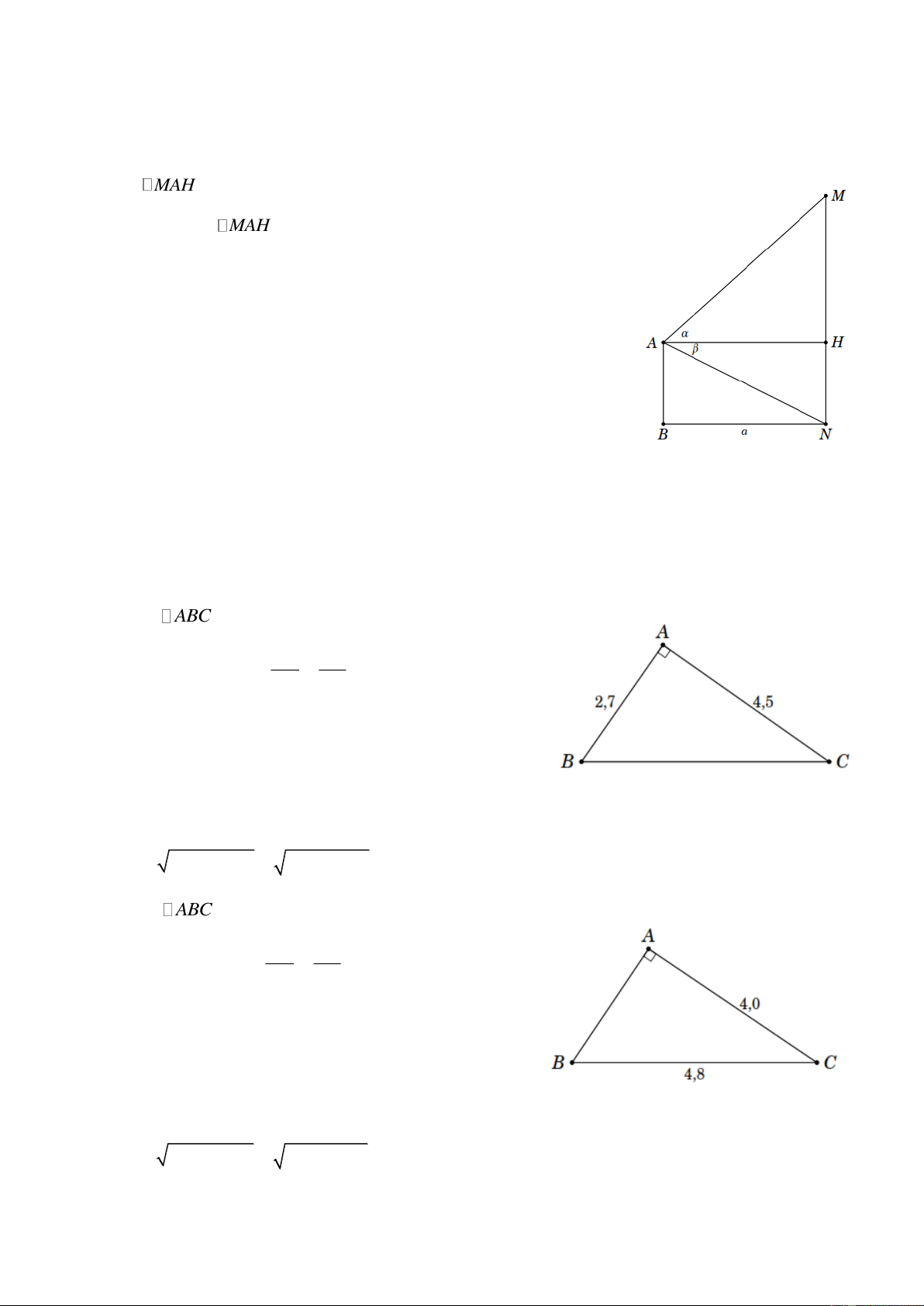
Ví dụ 15. Khoảng cách giữa hai chân tháp AB và MN là a như hình vẽ bên dưới. Từ đỉnh A của
tháp AB nhìn lên đỉnh M của tháp MN ta được góc  . Từ đỉnh A nhìn xuống chân N của tháp Trang 6
MN ta được góc  (so với phương nằm ngang AH ). Hãy tìm chiều cao MN nếu a  120m ,  30  ,  20  . Lời giải
Xét MAH vuông tại H , ta có HM  AH  tan .
Tương tự, xét MAH vuông tại H , ta có HN  AH  tan  . Mà MN
 HM  HN  AH  tan  AH  tan 
 AH tan  tan  
 120tan30  tan 20  113,0m.
Vậy chiều cao MN là 113, 0m .
C. BÀI TẬP VẬN DỤNG
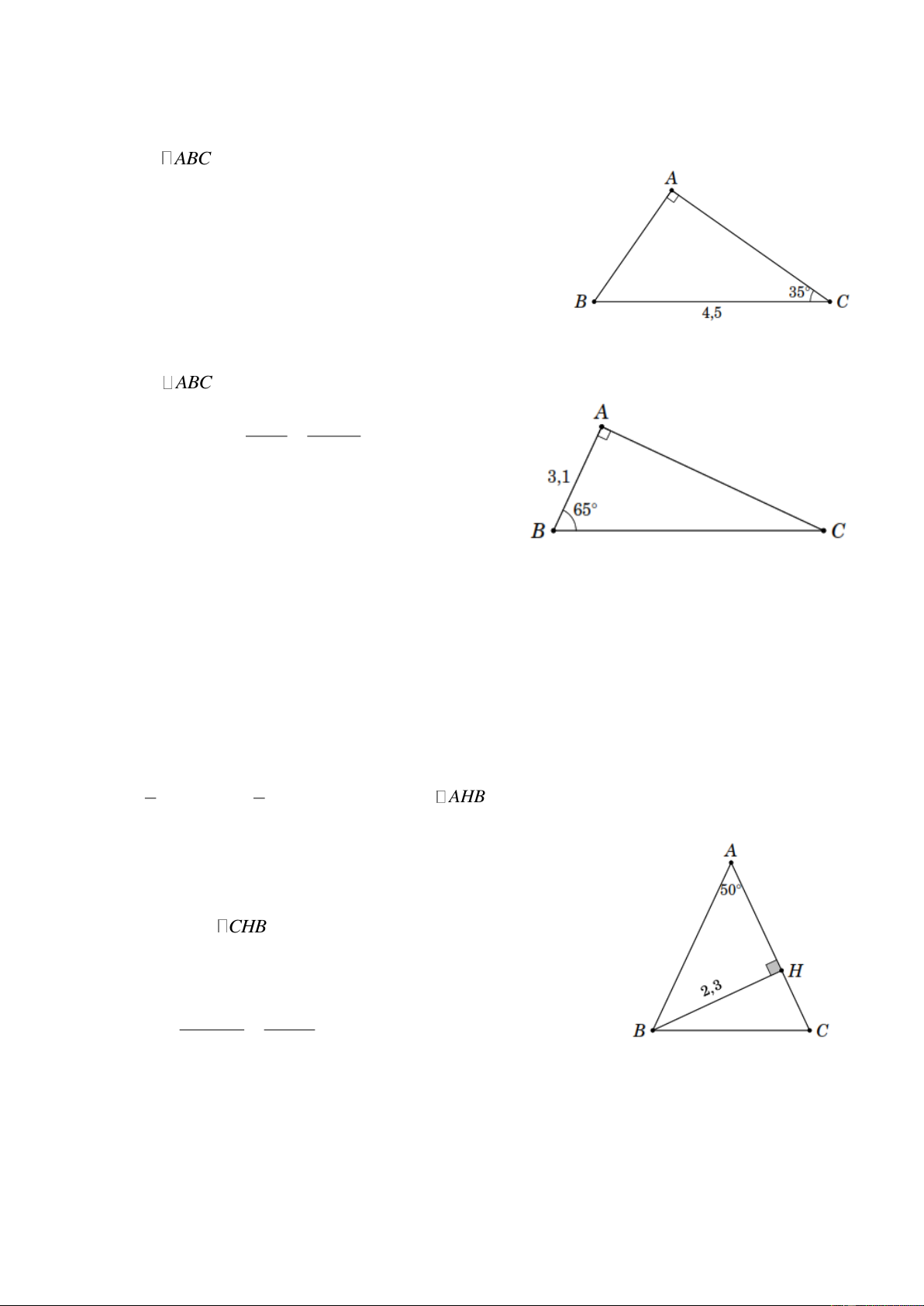
Bài 1. Giải tam giác ABC vuông tại A , biết
a) AB  2, 7 và AC  4, 5 ;
b) AC  4, 0 và BC  4,8 . Lời giải
a) Xét ABC vuông ở A , ta có AC 4,5 tan B    tan 5904 AB 2, 7 Suy ra ˆ B  5904 mà ˆ ˆ B C 90   nên ˆ  ˆ
C  90  B  90  5904  30  56 . 
Mặt khác, theo định lí Py-ta-go ta có 2 2 2 2 BC 
AB  AC  2, 7  4,5  5, 25.
b) Xét ABC vuông ở A , ta có AC 4, 0 sin B    sin 5644 BC 4,8 Suy ra ˆ B  5644 mà ˆ ˆ B C 90   nên ˆ  ˆ
C  90  B  90  5644  33 1   6 . 
Mặt khác, theo định lí Py-ta-go ta có 2 2 2 2 AB 
BC  AC  4,8  4, 0  2, 65.
Bài 2. Giải tam giác ABC vuông tại A , biết Trang 7 a) BC  4, 5 và ˆ C 35  ; b) AB  3,1 và ˆ B 65  . Lời giải
a) Xét ABC vuông ở A , ta có AB BC sin C 4,5 sin 35      2,58 .
Tương tự, AC BC cosC 4,5 cos35      3,69 . Do ˆ ˆ B C 90   nên ˆ  ˆ B 90 C 90 35 55 .      
b) Xét ABC vuông ở A , ta có AB 3,1 BC    7,34 . cos B cos 65 Tương tự, AC AB tan B 3,1 tan 65      6,65 . Do ˆ ˆ B C 90   nên ˆ  ˆ C 90 B 90 65 25 .      
Bài 3. Cho tam giác ABC cân tại A , đường cao BH . Biết ˆ A 50 
, BH  2, 3 . Tính chu vi của ABC  . Lời giải Do giả thiết suy ra ˆ ˆ B  C nên 1 C   A 1 ˆ ˆ 180 180 50 65 .     
Xét AHB vuông tại H , ta 2 2 có AH BH cot HAB 2,3 cot 50     1,92.
Tương tự, xét CHB vuông tại H , ta có CH BH cot HCB 2,3 cot 65     1,07. BH 2, 3 và BC    2,54  . sin HCB sin 65
Mà AC  AH  HC  1, 92 1, 07  2, 99 . Do đó chu vi tam giác ABC bằng
AB  BC  CA  2  2, 99  2, 54  8, 52.
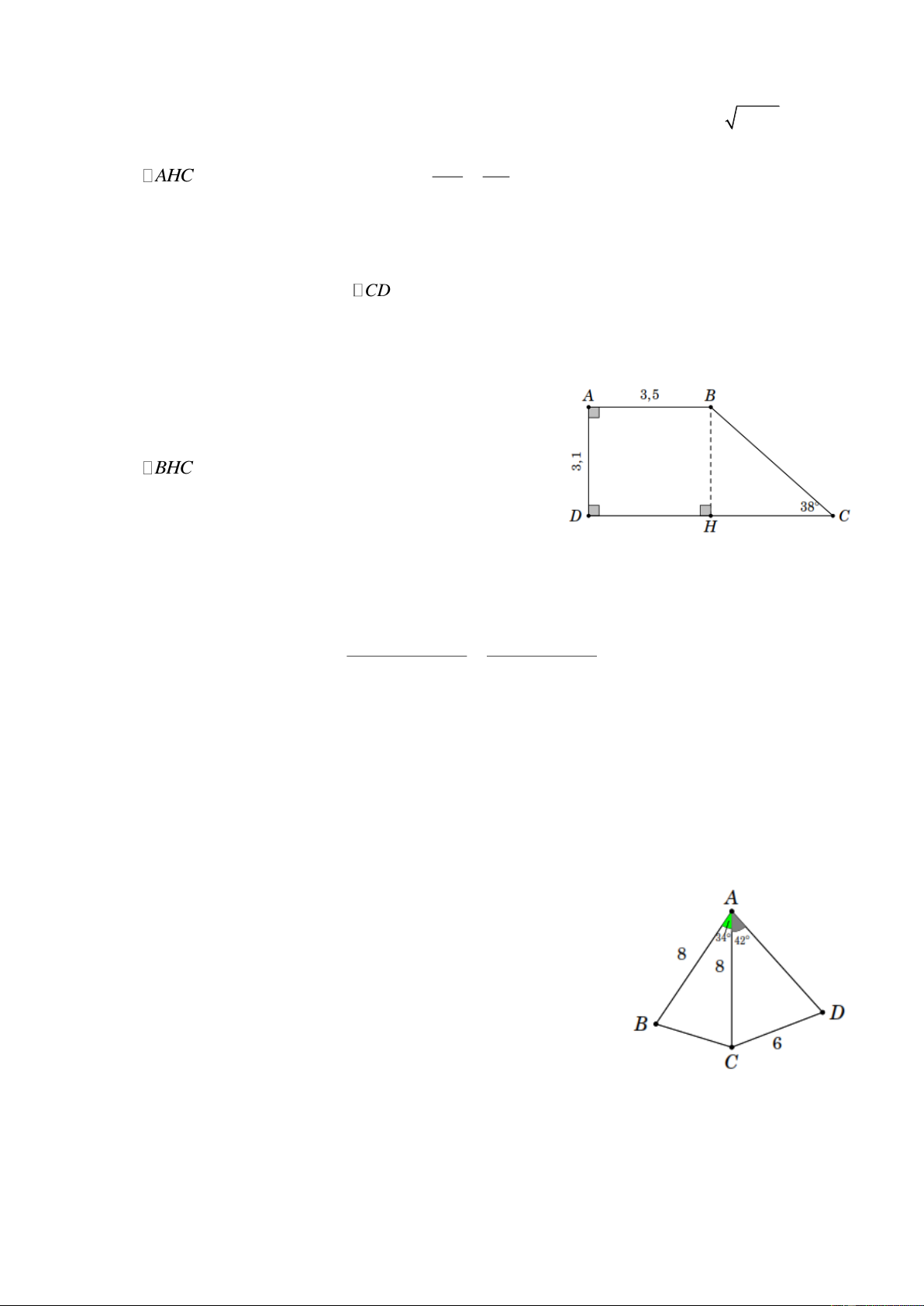
Bài 4. Hình thang ABCD có ˆ ˆ A D 90  
. Biết AB  2, 6 , CD  4, 7 và ˆ C 35  . Tính diện tích hình thang. Trang 8 Lời giải
Vẽ BH  CD , do giả thiết suy ra ABHD là hình chữ nhật nên AB  DH  2, 6 .
Mà CD  DH  HC  HC  DC  DH  4, 7  2, 6  2,1 .
Xét BHC vuông tại H , ta có BH HC tan BCH 2,1 tan 35     1,5.
Gọi S là diện tích hình thang ABCD .
AB CDBH 2,6 4,71,5 Ta có S    5,5. 2 2
Bài 5. Cho tam giác nhọn ABC , AB  AC , đường cao AH và đường trung tuyến AM . Gọi  là số đo góc HAM .
a) Chứng minh rằng HB  HC  2HM ; cot B cot C b) Chứng minh rằng tan    . 2 Lời giải
a) Do giả thiết AM là trung tuyến nên BM  MC .
Mà HB  HC  HM  BM   MC  MH   2 MH.
b) Đặt AH  h , xét AHB , ta có HB  AH  cot ABH  h  cot ABH .
Tương tự, xét AHC , ta có HC  AH cot ACH  hcot ACH .
Suy ra HB  HC  h  cot ABH  cot ACH  hay 2HM  hcot B  cot C . (1)
Mặt khác, xét AMH vuông tại H , ta có HM  h  tan MAH  h  tan
hay 2HM  2h tan . (2) B C
Từ (1) và (2) suy ra h  h  B C  cot cot 2 tan cot cot tan         . 2
Bài 6. Giải tam giác nhọn ABC biết ˆ B 60 
, AB  3, 0 và BC  4, 5 . Lời giải
Kẻ đường cao AH  BC . Xét ABH vuông tại H , ta có AH AB sin B 3, 0 sin 60      2,6 . Tương tự, xét BH AB cos B 3, 0 cos 60     1,5 . Trang 9
Mà HC  BC  BH  4, 5 1, 5  3, 0 .
Theo định lí Py-ta-go ta có 2 2 2 2 2
AB  BH  AH  3, 0  2, 6  15, 76 suy ra AB  15, 76  4, 0 . AH 2, 6 Xét AHC vuông tại 
H ta có tan ACH    tan 40 55 . HC 3, 0 Do ˆ  ˆ ˆ
A  180  B  C  180  60  40 5  5   79 5  .
Bài 7. Hình thang ABCD ( AB CD ) có ˆ D 90  , ˆ C 38 
, AB  3, 5 , AD  3,1. Tính diện tích hình thang đó. Lời giải
Vẽ BH  CD , do giả thiết suy ra ABHD là hình chữ
nhật. Do đó BH  3,1, DH  3, 5 .
Xét BHC vuông tại H , ta có HC BH cot C 3,1 cot 38      4,0.
Mà CD  DH  HC  3, 5  4, 0  7, 5 .
Gọi S là diện tích hình thang ABCD khi đó
AB CDBH 3,5 7,53,1 S   17,1. 2 2
D. BÀI TẬP TỰ LUYỆN
Bài 8. Các cạnh của một tam giác vuông có độ dài 4cm; 6cm và 6cm. Hãy tính góc nhỏ nhất của tam giác đó.
Bài 9. Tam giác ABC vuông tại A có AB  21 cm, ˆ C 40  . Hãy tính các độ dài a) AC ; b) BC ; c) Phân giác BD .
Bài 10. Cho hình bên, biết: AB  AC  8 cm, CD  6 cm, BAC 34  
và CAD  42 . Hãy tính
a) Độ dài cạnh BC ; b) ADC ;
c) Khoảng cách từ điểm B đến cạnh AD . 
Bài 11. Trong một tam giác ABC có AB  11cm, ABC  38 , ACB 30 
, N là chân đường vuông góc kẻ từ A đến BC . Hãy tính AN , AC .
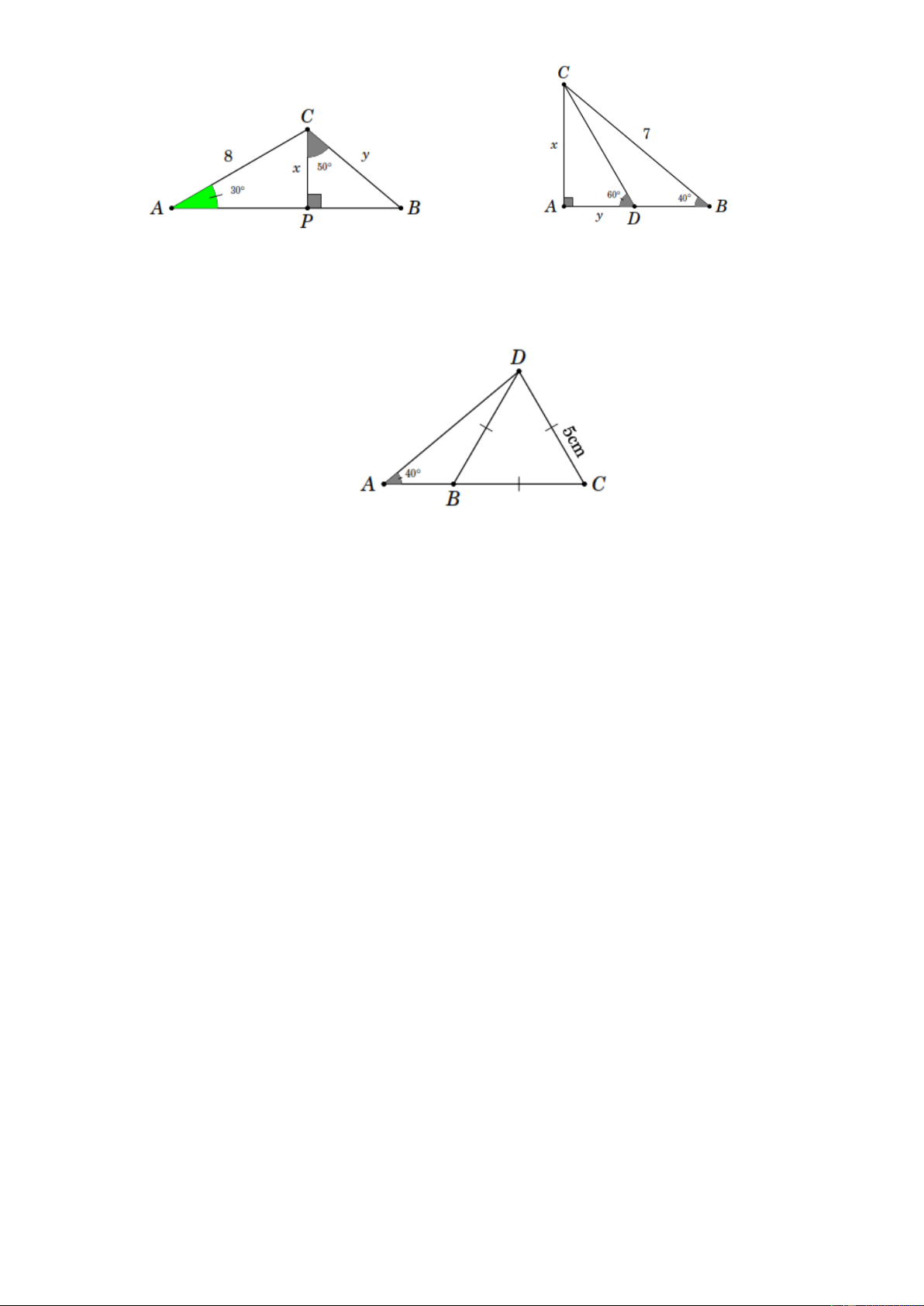
Bài 12. Tìm x và y trong các hình sau Trang 10 Bài 13. Cho tam giác 
BCD đều cạnh 5 cm và DAB  40 . Hãy tính a) AD ; b) AB . --- HẾT --- Trang 11