Phương pháp giải hình 9 hệ thức về cạnh và đường cao trong tam giác vuông (có đáp án và lời giải chi tiết)

Chương 1
Bài 1. MỘT SỐ HỆ THỨC VỀ CẠNH
VÀ ĐƯỜNG CAO TRONG TAM GIÁC VUÔNG
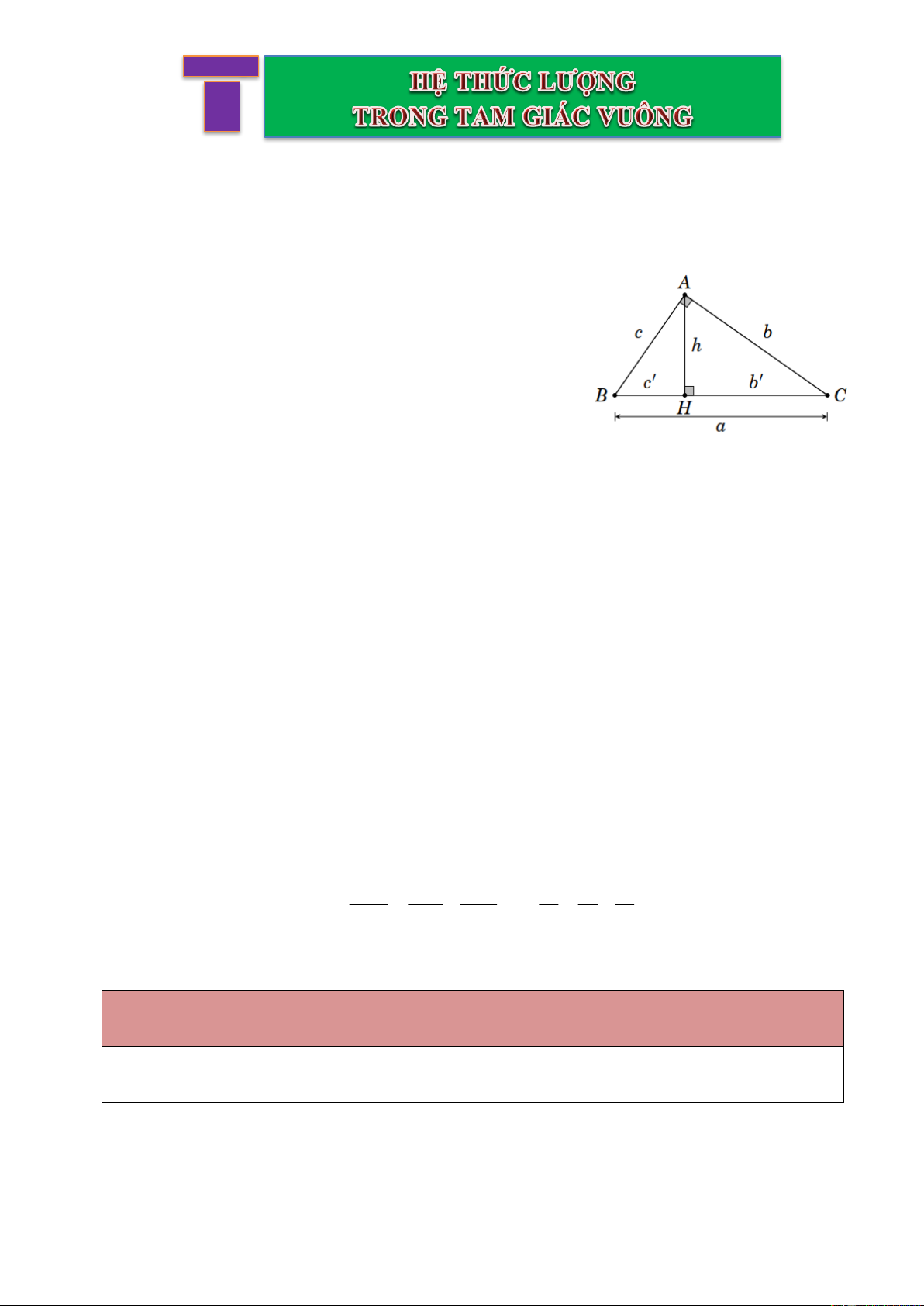
A. KIẾN THỨC TRỌNG TÂM Mở đầu Từ hình vẽ bên, ta có
 Cạnh góc vuông: AB, AC .
 Cạnh huyền: BC .
 Đường cao: AH .
 HA là hình chiếu của AB trên cạnh BC .
 HC là hình chiếu của AC trên cạnh BC .  Định lý Py-ta-go: 2 2 2
BC  AB  AC
1. Hệ thức liên hệ giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền
 Trong tam giác vuông, bình phương mỗi cạnh góc vuông bằng tích của cạnh huyền và hình
chiếu của nó trên cạnh huyền. 2
BA  BH  BC hay 2
c  c ' a ; 2
CA  CH  CB hay 2
b  b ' a .
2. Hệ thức liên quan đến đường cao Trong một tam giác vuông
 Bình phương độ dài đường cao bằng tích hình chiếu của hai cạnh góc vuông trên cạnh huyền. 2
AH  HB  HC hay 2
h  b ' c ' .
 Tích độ dài đường cao với cạnh huyền bằng tích độ dài hai cạnh góc vuông.
AH  BC  AB AC hay a  h  bc .
 Nghịch đảo bình phương độ dài đường cao bằng tổng nghịch đảo bình phương độ dài hai cạnh góc vuông. 1 1 1   1 1 1 hay   . 2 2 2 AH AB AC 2 2 2 h a b
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1: Tính độ dài đoạn thẳng và các yếu tố khác dựa vào hệ thức liên hệ giữa cạnh góc vuông
và hình chiếu của nó trên cạnh huyền
 Vận dụng định lý Py-ta-go để tính cạnh thứ ba (nếu cần).
 Vận dụng các hệ thức liên hệ giữa cạnh và đường cao trong tam giác.
Ví dụ 1. Tính các độ dài x , y trong hình bên. Trang 1 a) b) c) Lời giải
a) Áp dụng định lí Pytago ta được 2 2 2 2 2
BC  AB  AC  7,5 10  156, 25. Do đó BC  12,5 . Áp dụng hệ thức 2
c  ac ta được 2 2
AB  BC  BH  7,5  12,5x  x  4,5.
Suy ra y  BC  BH  12, 5  4, 5  8 .
b) Ta có BC 1 3  4 . Áp dụng hệ thức 2
c  ac ta được 2 2
AB  BC  BH  x  4 1  4  x  2; 2 2
AC  BC CH  y  3 4  y  2 3. c) Áp dụng hệ thức 2
c  ac ta được
AB  BC  BH   2 2 2 5
 (x  6)6  x  6 10  x  4 4
Ví dụ 2. Một tam giác vuông có tỉ số hai cạnh góc vuông bằng
. Tính tỉ số hai hình chiếu của hai 9
cạnh góc vuông đó trên cạnh huyền. Lời giải
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền, ta có 2 b  ab ; 2 b ab b 2
c  ac , suy ra   2 c ac c . 2 b 4 b  4  16 Nếu  thì     . c 9 c  9  81 3
Ví dụ 3. Một tam giác vuông có tỉ số hai cạnh góc vuông bằng
, cạnh huyền dài 10 cm. Tính độ 4
dài các hình chiếu của hai cạnh góc vuông trên cạnh huyền. Trang 2 Lời giải
Áp dụng hệ thức (1) ta có 2 b  ab ; 2 c  ac 2 b ab b Suy ra   2 c ac c . b 3 b 9 b c b  c 10 2 Nếu  thì      . c 4 c suy ra 16 9 16 9 16 25 5 Do đó 2 2 b 
9  3,6 ; c  16  6, 4 . 5 5
Dạng 2: Tính độ dài dựa vào hệ thức liên quan đến đường cao
 Vận dụng các hệ thức liên quan đến đường cao và định lý Py-ta-go.
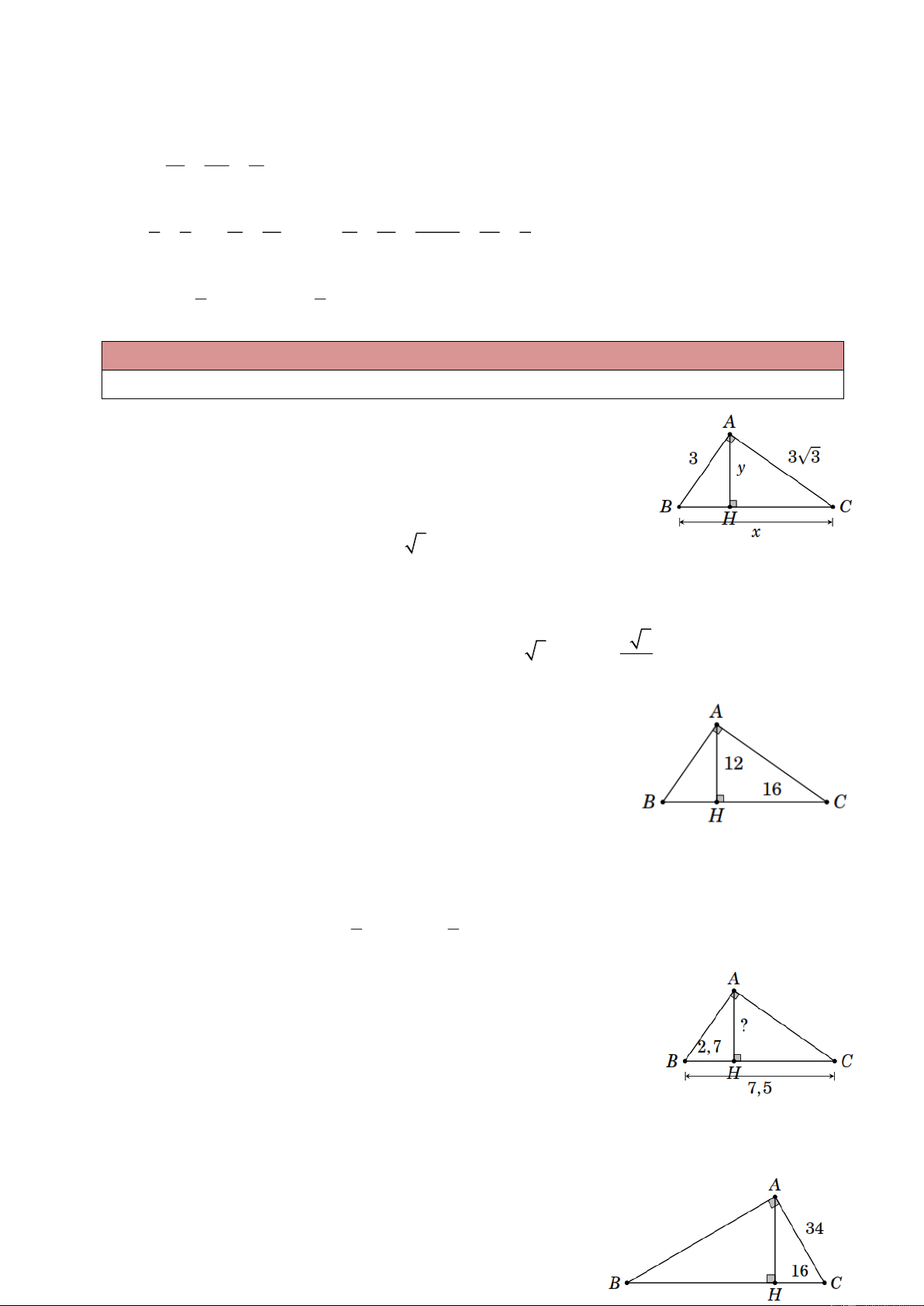
Ví dụ 4. Tính độ dài x , y trong hình bên. Lời giải
Áp dụng định lí Pytago ta được
BC  AB  AC    2 2 2 2 2 3 3 3  36  x  6.
Áp dụng hệ thức ah  bc ta được 3 3
AH  BC  AC  AB  6 y  3 3  3  y  . 2
Ví dụ 5. Tính diện tích tam giác ABC trong hình bên. Lời giải Áp dụng hệ thức 2 h  b c   ta được 2 2
AH  HB  HC  12  BH 16  BH  9.
Do đó BC  916  25. 1 1
Diện tích tam giác ABC là S  BC  AH   2512  150 (đvdt). 2 2
Ví dụ 6. Tính độ dài AH trong hình bên. Lời giải
Ta có HC  7, 5  2, 7  4,8 . Áp dụng hệ thức 2 h  b c   ta được 2
AH  BH  HC  2, 7  4,8  12,96  AH  3, 6 .
Ví dụ 7. Tính tích HA HB HC trong hình bên. Trang 3 Lời giải Ta có 2 2 2 2 2
AH  AC  HC  34 16  900  AH  30 . Vậy 2 3 3
HA  HB  HC  HA  HA  HA  30  27000 .
Dạng 3: Chứng minh các hệ thức hình học
 Vận dụng linh hoạt các hệ thức liên quan đến cạnh và đường cao trong tam giác vuông.
 Nếu cần thì có thể vẽ thêm đường phụ (thường là đường cao) sao cho hình vẽ xuất hiện
tam giác vuông để vận dụng các hệ thức.
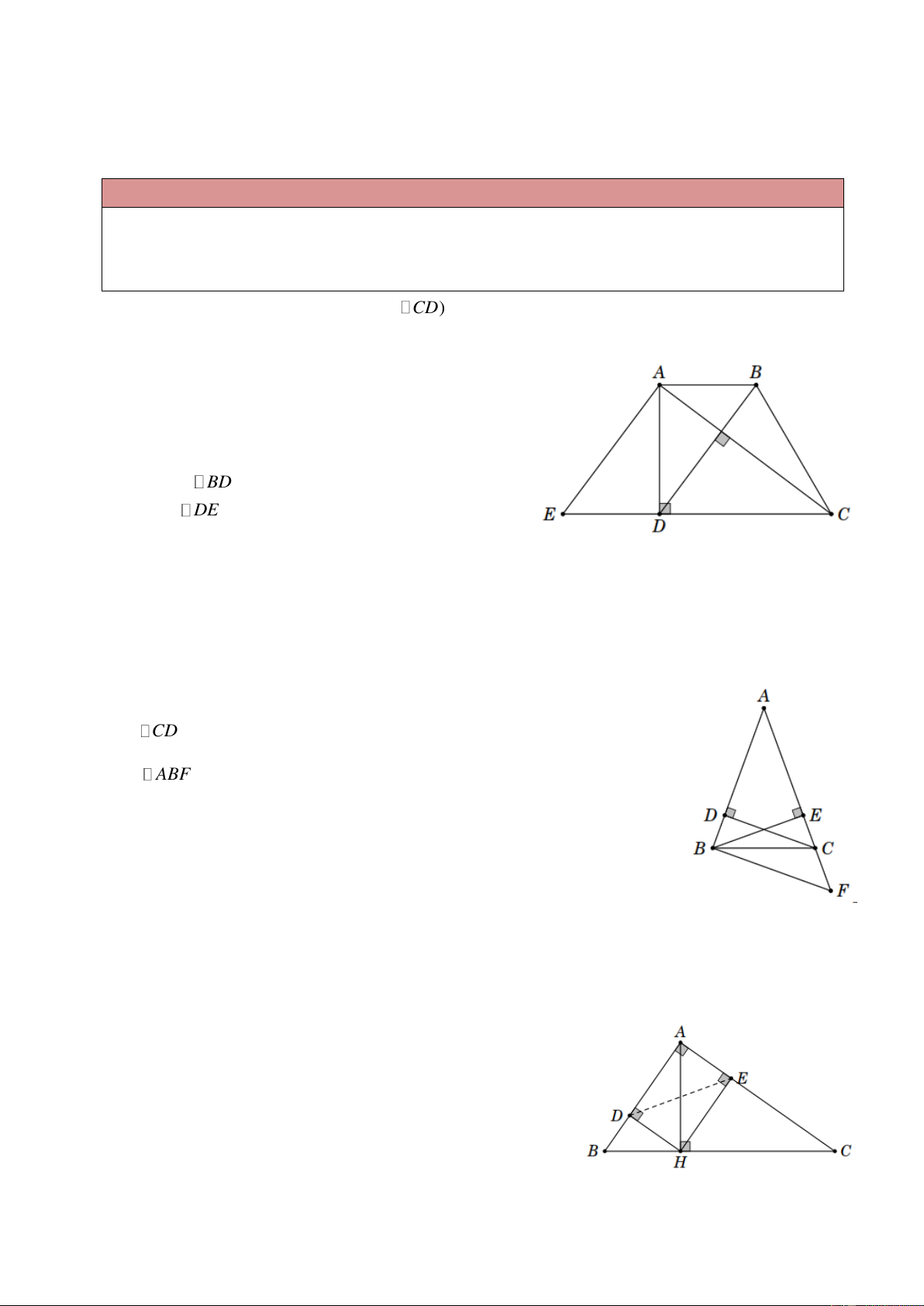
Ví dụ 8. Cho hình thang ABCD ( AB CD) có ˆ D 90 
và AC  BD . Chứng minh rằng AD là
trung bình nhân của hai đáy. Lời giải
Qua A vẽ đường thẳng vuông góc với AC và cắt
đường thẳng CD tại E (hình bên).
Ta có AE BD (vì cùng vuông góc với AC ). Mặt
khác AB DE nên tứ giác ABDE là hình bình hành.
Suy ra DE  AB . Áp dụng hệ thức 2 h  b c   ta có 2
AD  DE  DC suy ra 2
AD  AB  DC (đpcm).
Ví dụ 9. Cho tam giác ABC cân tại A . Vẽ các đường cao BE và CD . Từ B vẽ một đường thẳng
song song với CD cắt tia AC tại F . Chứng minh rằng 2
AC  AE  AF . Lời giải
BF CD mà CD  AB nên BF  AB (hình bên).
Xét ABF vuông tại B có BE là đường cao ứng với cạnh huyền AF nên 2
AB  AE  AF . Suy ra 2
AC  AE  AF (vì AB  AC ).
Ví dụ 10. Cho tam giác ABC vuông tại A , đường cao AH . Gọi D và E
lần lượt là hình chiếu của H trên AB và AC . Chứng minh rằng 3
DE  BD  CE  BC . Lời giải Áp dụng hệ thức 2
b  ab vào các tam giác vuông HAB và HAC ta được 2
BH  AB  BD ; 2
HC  AC  CE . Mặt khác 2 4 2 2
AH  HB  HC  AH  HB  HC  AB  BD  AC CE .
Nhưng AB AC  BC  AH nên 4 3
AH  BD CE  BC  AH  AH  BD CE  BC . Trang 4
Dễ thấy tứ giác ADHE là hình chữ nhật nên AH  DE . Do đó 3
DE  BD  CE  BC .
Ví dụ 11. Cho tam giác ABC cân tại A , hai đường cao AD và BE . Cho biết BE  2k ; BC  2m; 1 1 1
AD  n . Chứng minh rằng   . 2 2 2 k m n Lời giải
Tam giác ABC cân tại A nên đường cao AD cũng là đường trung
tuyến, do đó DB  DC  m .
Vẽ DH  AC thì DH
BE và DH là đường trung bình của EBC (hình bên), do đó 1 DH  BE  k . 2 1 1 1 Áp dụng hệ thức  
vào DAC vuông tại D , ta được 2 2 2 h b c 1 1 1 1 1 1      . 2 2 2 2 2 2 DH DC AD k m n
C. BÀI TẬP VẬN DỤNG
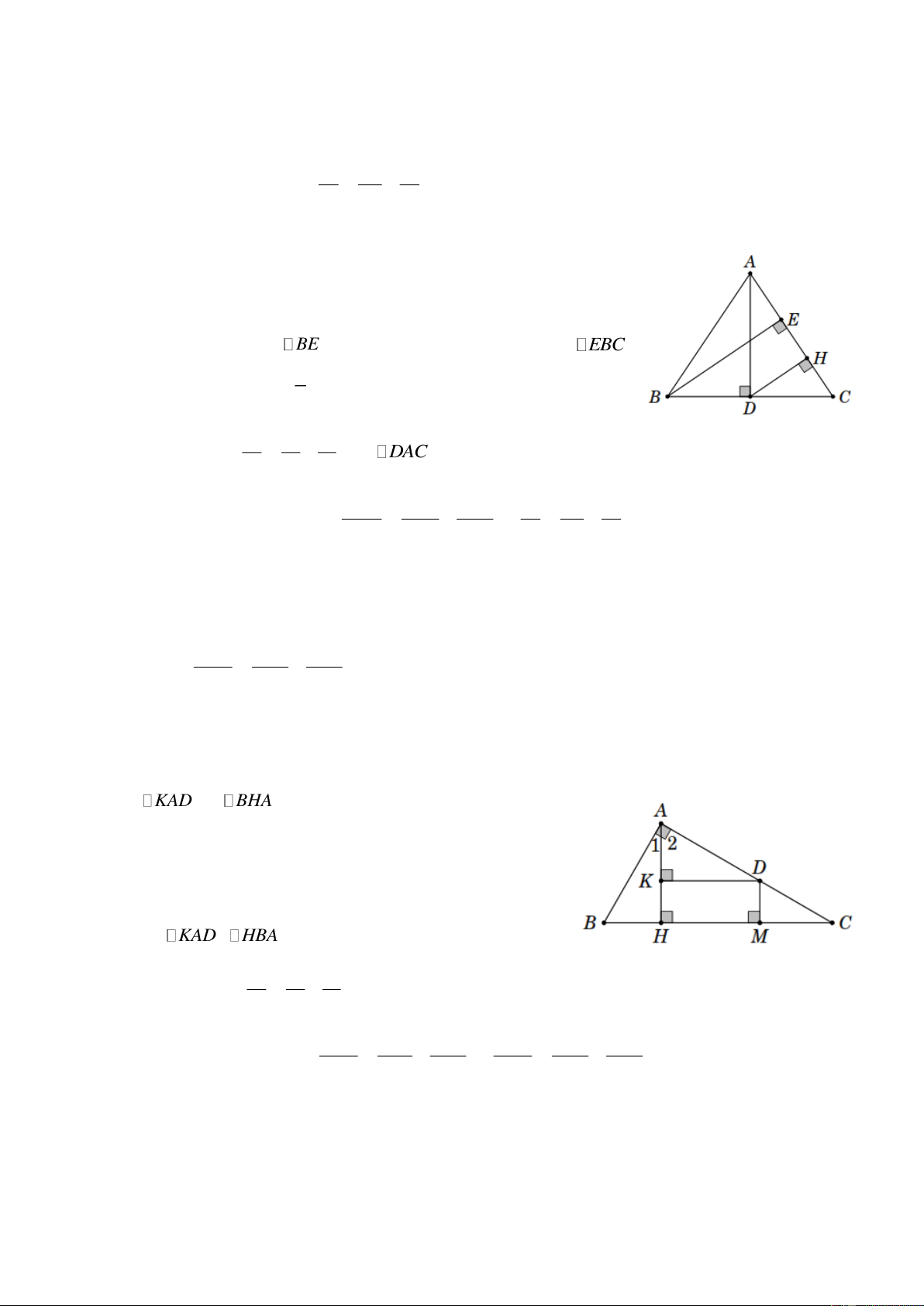
Bài 1. Cho tam giác ABC vuông tại A ( AB  AC) , đường cao AH . Lấy điểm M trên đoạn thẳng
HC sao cho HM  AH . Qua M vẽ một đường thẳng vuông góc với BC , cắt AC tại D . Chứng 1 1 1 minh rằng   . 2 2 2 AH AD AC Lời giải
Vẽ DK  AH (hình bên), tứ giác KDMH là hình chữ nhật nên KD  MH , do đó KD  AH .
Xét KAD và BHA có ˆ ˆ K H 90   ; KD  AH ; ˆ ˆ
A  B (cùng phụ với ˆ A ). 2 1
Do đó KAD  HBA (g.c.g) suy ra AD  AB . 1 1 1 Áp dụng hệ thức   ta được 2 2 2 h b c 1 1 1 1 1 1      . 2 2 2 2 2 2 AH AB AC AH AD AC
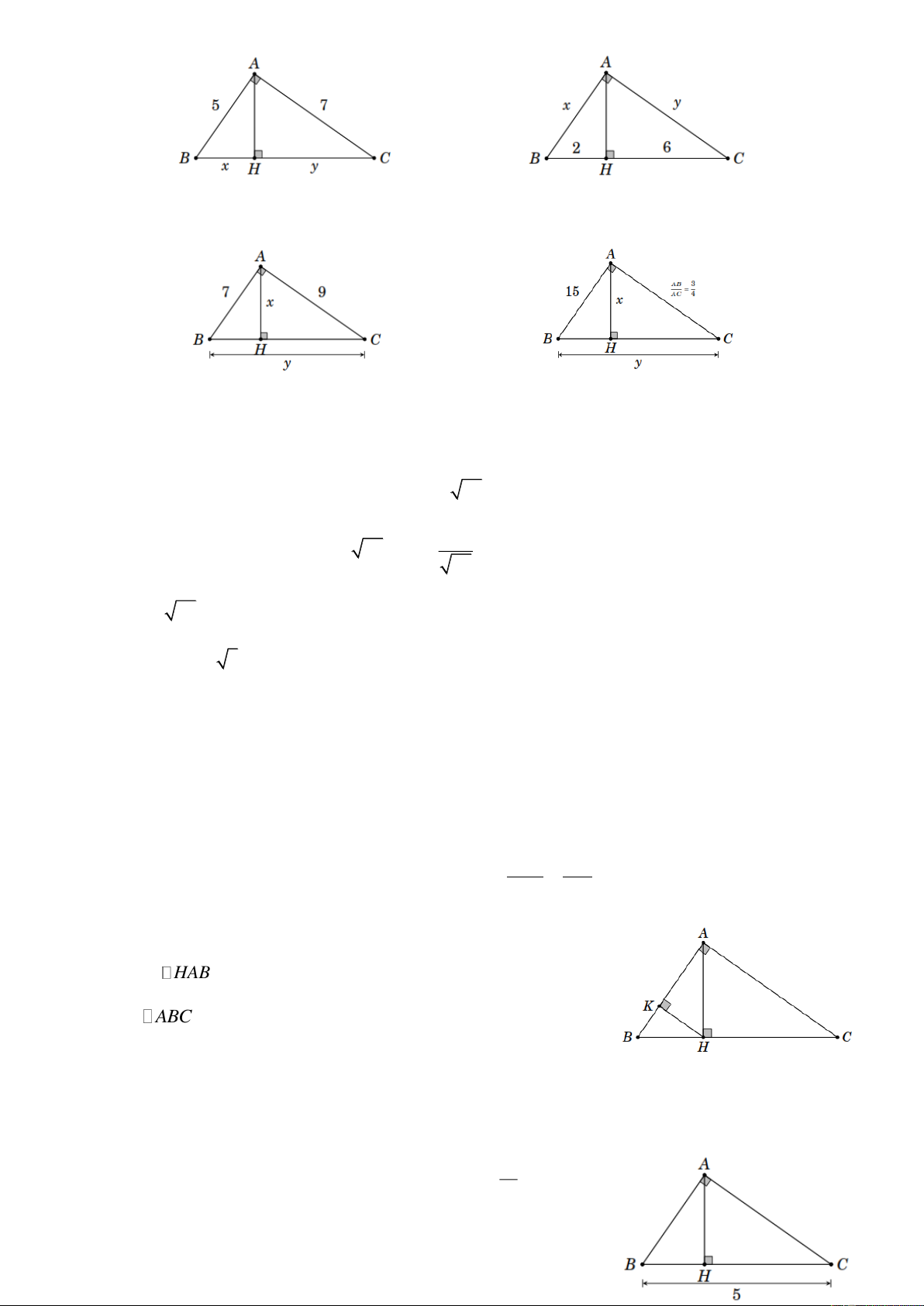
Bài 2. Tính x , y trong hình vẽ sau Trang 5 a) b) c) d) Lời giải
a)  x  y2 2 2
 5  7  25 49  74  x  y  74 . 25 Ta có 2 2
BA  BH  BC  5  x  74  x   2,9 . 74
 y  74  2,9  5,7 .
b) x  4; y  4 3 .
c) x  5, 5; y  11, 4 .
d) AC  20; x  12; y  25 .
Bài 3. Cho tam giác ABC vuông tại A , đường cao AH . Vẽ HK  AB (K  AB) . Chứng minh rằng 2 AB HB
a) AB AK  BH  HC ; b)  . 2 AC HC Lời giải
a) Xét HAB vuông tại H có 2
AH  AB  AK .(1)
Xét ABC vuông tại A ta có 2
AH  BH  HC .(2)
Từ (1) và ( 2 ) suy ra AB AK  HB HC . b) Tính 2 AB ; 2
AC rồi lập tỉ số của chúng và rút gọn ta được điều phải chứng minh.
Bài 4. Cho tam giác ABC vuông tại A , cạnh BC  5 cm và tỉ số 9
hai hình chiếu của AB , AC trên cạnh huyền bằng . Tính diện 16 tích tam giác ABC . Trang 6 Lời giải
Vẽ AH  BC , tính được HB  1,8 cm; HC  3, 2 cm. Từ đó tính được AH  2, 4 cm. Diện tích ABC là 2 6cm .
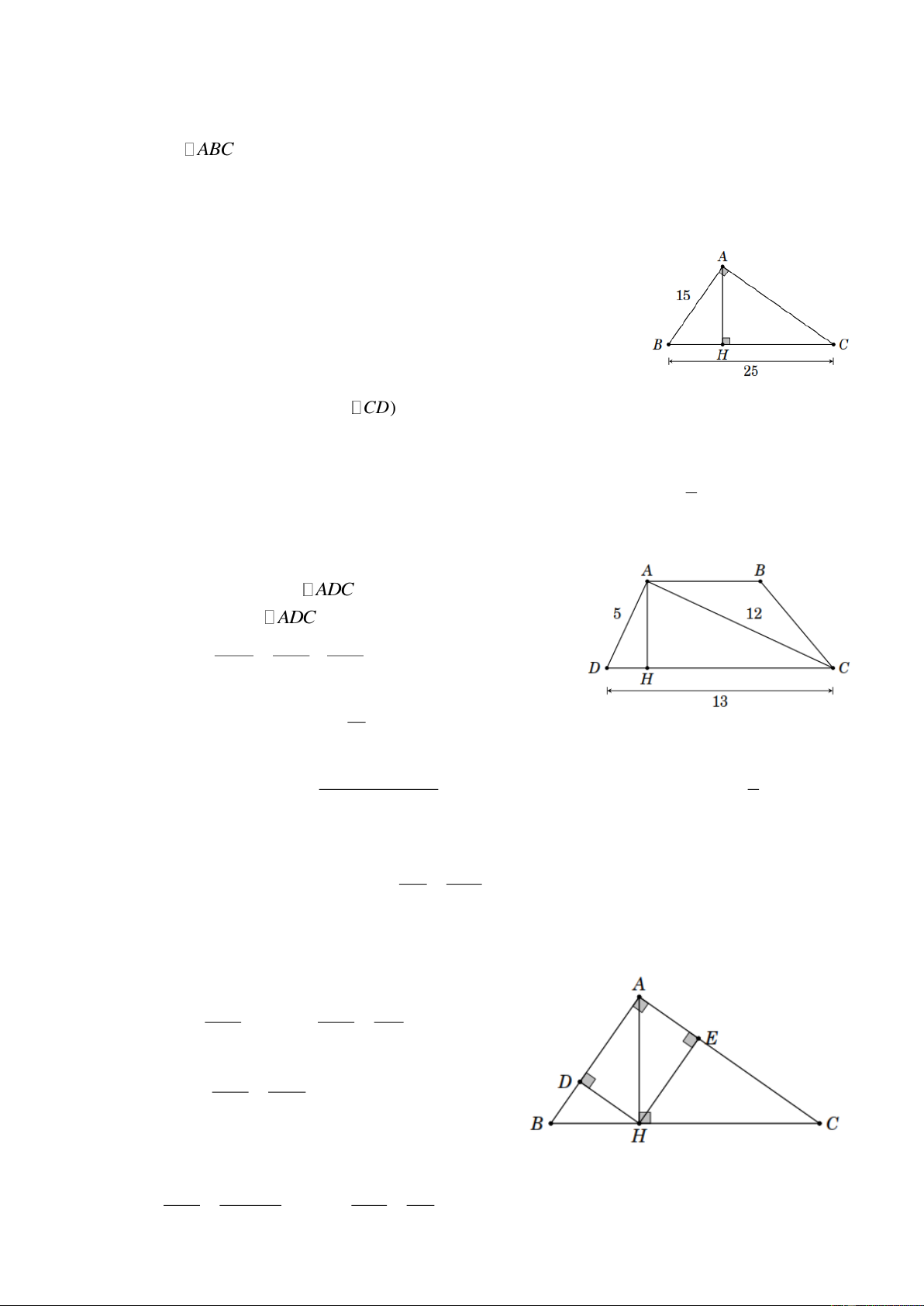
Bài 5. Cho tam giác ABC vuông tại A , AB 15cm; BC  25cm. Tính độ dài hai hình chiếu của
hai cạnh góc vuông trên cạnh huyền và tính đường cao tương ứng với cạnh huyền. Lời giải Vận dụng hệ thức 2
c  ac , tính được BH  9cm, từ đó suy ra CH 16cm. Vận dụng hệ thức 2 h  b c
  , ta tính được AH 12 cm.
Bài 6. Hình thang ABCD ( AB CD) có AD  5cm; AC 12cm và CD 13 cm. Biết diện tích hình thang là 2 45cm . 1
a) Tính chiều cao của hình thang.
b) Chứng minh rằng AB  CD . 2 Lời giải
a) Vẽ AH  BC . Xét ADC có 2 2 2
AD  AC  CD (vì 2 2 2 5 12  13 ) nên
ADC là tam giác vuông tại A . Vận 1 1 1 dụng hệ thức   , ta tính được 2 2 2 AH AD AC 8 AH  4 cm. 13
( AB  CD)  AH
b) Vận dụng công thức S 
, ta tính được AB  6,5 cm. Do đó 1 AB  CD . 2 2
Bài 7. Cho tam giác ABC vuông tại A , đường cao AH . Vẽ HD  AB , HE  AC 3 BD AB
(D  AB, E  AC) . Chứng minh rằng  . 3 CE AC Lời giải
Trước hết, vận dụng các hệ thức 2 b  ab ; 2 c  ac 2 2 để AB AB HB tính tỉ số , ta được  . 2 AC 2 AC HC 4 2 AB HB Từ đó suy ra  . 4 2 AC HC Ta có 2
HB  AB  BD ; 2
HC  AC  CE . 4  3 Do đó AB AB BD  AB BD . Suy ra  .--- HẾT --- 4 AC AC CE 3 AC CE Trang 7