Tài liệu Toán 9 chủ đề một số hệ thức về cạnh và đường cao trong tam giác vuông

Tài liệu gồm 43 trang, bao gồm kiến thức cần nhớ, các dạng toán và bài tập chủ đề một số hệ thức về cạnh và đường cao trong tam giác vuông trong chương trình môn Toán 9, có đáp án và lời giải chi tiết. Mời bạn đọc đón xem.

51 26 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Hệ thức lượng trong tam giác vuông

Môn: Toán 9

Thông tin:

43 trang 6 tháng trước

Tác giả:

Profile Hà Việt Anh
1
ÔN TẬP HỆ THỨC VỀ CẠNH VÀ ĐƯỜNG CAO TRONG TRONG TAM GIÁC
VUÔNG
A. Tóm tắt lý thuyết
Khi giải các bài toán liên quan đến cạnh và đường cao trong tam giác vuông, ngoài việc nắm
vững các kiến thức về định lý Talet, về các trường hợp đồng dạng của tam giác, cần phải nắm
vững các kiến thức sau:
Tam giác
ABC
vuông tại
A
, đường cao
AH
, ta có:
1) Hệ thức giữa cạnh góc vuông và hình chiếu của
nó trên cạnh huyền
Định lí 1: Trong một tam giác vuông, bình phương
mỗi cạnh góc vuông bằng tích của cạnh huyền và
hình chiếu của cạnh góc vuông đó trên cạnh huyền
Ta có:
2
.
AB BH BC=
;
2
.
AC HC BC=
2) Hệ thức liên qua tới đường cao
Định lí 2: Trong một tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng tích
hai hình chiếu của hai cạnh góc vuông trên cạnh huyền
Ta có:
2
.
AH BH HC=
Định lí 3: Trong một tam giác vuông, tích hai cạnh góc vuông bằng tích của cạnh huyền và
đường cao tương ứng
Ta có:
..AB AC AH BC
=
Định lí 4: Trong một tam giác vuông, nghịch đảo của bình phương đường cao ứng với cạn
huyền bằng tổng các nghịch đảo của bình phương hai cạnh góc vuông
Ta có:
*) Tóm tắt các công thức
1)
2 22
a bc
. 2)
22
. '; . 'babcac
3)
2
'. 'h bc
4)
..ah bc
.
5)
2 22
1 11
h bc

.
b'
c'
h
c
b
a
H
C
B
A
2
Chú ý: Diện tích tam giác vuông:
1
2
S ab
B. Bài tập và các dạng toán
Dạng 1: Tính độ dài các đoạn thẳng trong tam giác vuông
Cách giải:
Bước 1: Xác định vai trò của đoạn thẳng đã biết và đoạn thẳng cần tính trong tam giác
vuông. Cụ thể, xác định xem đoạn thẳng đó là
+) Là cạnh góc vuông +) Là đường cao
+) Là cạnh huyền +) Là hình chiếu
Bước 2: Từ đó lựa chọn công thức tính phù hợp (trong 6 công thức ở phần lý thuyết)
*) Lưu ý: Đôi khi phải dùng kĩ thuật đại số hóa để giải
Chẳng hạn:
- Nếu có
AB m
AC n
=
thì đặt
( )
,, 0
AB AC
k m n k AB km
mn
= = >⇒ =
và
AC kn=
- Nếu có
BH x CH BC BH BC x
=⇒=−=−
Bài 1: Tính
,
xy
trong mỗi hình vẽ sau
Lời giải
a) Xét
ABC∆
vuông tại
,A
đường cao
( )
AH H BC∈
, ta có:
y
x
8
6
C
H
B
A
y
x
7
5
C
H
B
A
Xác định vai trò
của các đoạn
thẳng
Lựa chọn công
thức tính phù hợp
3
Dùng định lý Pytago tính được
( )
10BC cm
=
(
)
( )
3, 6
6, 4
x cm
y cm
=
⇒
=
b) Xét
ABC∆
vuông tại
,A
đường cao
( )
AH H BC
∈
, ta có:
Dùng định lý Pytago tính được
(
)
74
BC cm=
( )
( )
35 74
74
74
x cm
y cm
=
⇒
=
Bài 2: Tính
,
xy
trong mỗi hình vẽ sau
Lời giải
a) Xét
ABC
∆
vuông tại
,A
đường cao
( )
AH H BC∈
, ta có:
( ) ( )
22
. 4 2 5 ; 25
AH HB HC AH AH x cm y cm= ⇔ =⇒ =⇒= =
b) Xét
ABC∆
vuông tại
,A
đường cao
( )
AH H BC∈
, ta có:
( )
( )
2
2
25 25 5 41
.;
74 4
AH
AH HB HC HC x cm y cm
HB
= ⇔ = = ⇒= =
Bài 3: Tính
,
xy
trong mỗi hình vẽ sau
Lời giải
y
x
4
1
C
H
B
A
y
x
5
7
C
H
B
A
y
x
5
10
C
H
B
A
y
x
32
30
C
H
B
A
4
a) Xét
ABC
∆
vuông tại
,A
đường cao
( )
AH H BC∈
, ta có:
Áp dụng hệ thức về cạnh ta có:
2
'.b ba=
, ta được:
( )
2
9
10 8 8
2
yy= + ⇔=
Áp dụng hệ thức về cạnh:
2
'.c ca
=
, ta được:
( )
2
2
9 9 15 15
80
22 2 2
x xx

= + = ⇔= >


b) Áp dụng hệ thức về cạnh:
2
'.c ca
=
, ta được:
( ) ( )(
)
( )
2
30 32 18 50 0 18 50 0
yy y y y y= +⇔− +=⇔= +>
Áp dụng hệ thức về cạnh:
2
'.b ba=
, ta được:
( ) ( )
2 22
32 32 18 40 40 0x x xx= + ⇔ = ⇔= >
.
Bài 4: Tính
,
xy
trong mỗi hình vẽ sau
Cho
ABC∆
vuông tại
A
, đường cao
( )
AH H BC∈
a) Cho biết
( )
( )
3, 5AB cm BC cm= =
. Tính
BH
,,CH AC AH
b) Cho biết
( ) ( )
9 , 16 .BH cm CH cm= =
Tính độ
dài các đoạn thẳng
,,,
AB AC BC AH
Lời giải
a) Xét
ABC
∆
vuông tại
,A
đường cao
( )
AH H BC
∈
, ta có:
+)
2
9
. 1,8() 3,2()
5
AB BH BC BH cm CH cm= ⇒== ⇒=
+)
22
. 5.3,2 16 4( )AC CB BC AC AC cm= ⇒ = =⇒=
+)
2 2 222
1 1 1 1 1 11
2, 4( )
3 4 9 16
AH cm
AH AB AC
= + =+=+⇒ =
b) Xét
ABC∆
vuông tại
,A
đường cao
( )
AH H BC∈
, ta có:
15 , 20 , 25 , 12AB cm AC cm BC cm AH cm= = = =
4
5
3
C
H
B
A
5
Bài 5:
Tính
,xy
trong mỗi hình vẽ sau, biết
5AH cm=
Lời giải
Xét
ABC∆
vuông tại
A
, đường cao
AH
Áp dụng hệ thức về cạnh và đường cao ta có:
+
( )
22
. 5. 5AH BH CH x x x cm= ⇒ = ⇒=
+
( )
2
2 2 2 2 22 2
1 1 1 111 12
50 5 2
5 25
y y cm
AH AB AC y y y
= + ⇒ = + ⇒ = ⇒ = ⇒=
.
Bài 6:
Cho
ABC∆
vuông tại
A
, đường cao
( )
AH H BC∈
, có
10 , 8AC cm AB cm= =
. Tính
,,,BC BH CH AH
Lời giải
a) Xét
ABC∆
vuông tại
,A
đường cao
( )
AH H BC∈
, ta có:
222
()BC AB AC pytago= +
2 41( )BC cm⇒=
+
2
2
64 32
. ()
2 41 41
AB
AB BH BC BH cm
BC
= ⇒= = =
+
32 50
2 41 ( )
41 41
CH BC BH cm=−= − =
+
2 2 22 2
1 1 1 11 11
6, 4( )
8 10 64 100
AH cm
AH AB AC
= + =+=+⇒=
10
8
C
H
B
A
5cm
x
x
y
y
H
C
B
A
6
Bài 7:
Cho
ABC∆
vuông tại
A
, đường cao
(
)
AH H BC∈
, có
10 , 42BH cm CH cm= =
. Tính
, ,,
BC AH AB AC
Lời giải
a) Xét
ABC
∆
vuông tại
,A
đường cao
( )
AH H BC∈
, ta có:
-
( )
10 42 52BC BH HC cm= + =+=
Áp dụng hệ thức lượng trong tam giác vuông ta có:
+)
2
. 10.52 520 2 130( )AB BH BC AB cm
= = =⇒=
+)
222
2 105( )AH AB BH AH cm= − ⇒=
+)
2 22
( ) 2 546( )AC AH HC pytago AC cm= + ⇒=
Bài 8:
Cho
ABC
∆
vuông tại
A
, đường cao
( )
AH H BC
∈
, có
10 , 42
BH cm CH cm= =
. Tính
, ,,BC AH AB AC
Lời giải
a) Xét
ABC∆
vuông tại
,A
đường cao
(
)
AH H BC∈
, ta có:
Áp dụng hệ thức lượng trong tam giác vuông ta có:
+)
22
2
2
12
. 16 4( )
9
AH
AH BH CH CH CH cm
BH
= ⇒= ==⇒=
+)
22
. 9.13 112 3 13( ); . 13.4 52 2 13( )AB BH BC AB cm AC BC CH AC cm= = =⇒= = = =⇒=
+)
2
11
. .12.13 78( )
22
ABC
S AH BC cm= = =
10
42
C
H
B
A
9
12
C
H
B
A
7
+) Chu vi
3 13 2 13 13 13 5 13( )
ABC AB BC CA cm∆ = + + = + +=+
Bài 9:
Cho tam giác
ABC
có
6, 8AB cm AC cm= =
và
10BC cm=
a) Chứng minh tam giác
ABC
vuông
b) Tính đường cao
AH
c) Gọi
,
MN
lần lượt là hình chiếu của
H
trên
,
AB AC
. Tính
,HM HN
Lời giải
a)
ABC∆
có
222
BC AB AC= +
(vì
2 22
10 6 8
= +
)
ABC⇒∆
vuông tại
A
(định lí pitago đảo)
b) Xét
ABC∆
vuông tại
A
, đường cao
AH
có:
..AB AC AH BC=
(hệ thức về cạnh và đường
cao)
( )
. 6.8
4,8
10
AB AC
AH cm
BC
⇒= ==
c) Xét
ABC∆
vuông tại
A
, đường cao
AH
có:
2
.AH BH BC
=
(hệ thức về cạnh và đường cao)
( )
22
6
3, 6
10
AB
BH cm
BC
⇒= ==
( )
10 3, 6 6, 4CH BC BH cm⇒ = = =−=
+ Vì
,MN
lần lượt là hình chiếu của
H
trên
,,AB AC HM AB HN AC⇒⊥ ⊥
+
AH BC⊥
AHB AHC⇒=
. Do đó các tam giác
,ABH ACH∆∆
vuông tại
H
+ Xét
ABH∆
vuông tại
H
, đường cao
HM
, có
..MH AB BH AH=
(hệ thức về cạnh và đường
cao)
( )
. 3,6.4,8
2,88
6
BH AH
MH cm
AB
⇒= = =
+ Xét
ACH
∆
vuông tại
H
, đường cao
HN
, có
..
HN AC AH CH=
(hệ thức về cạnh và đường
cao)
( )
. 6, 4.4,8
3,84
8
CH AH
NH cm
AC
⇒= = =
.
C
N
H
B
M
A
8
Bài 10:
Cho tam giác
ABC
vuông tại
A
, đường cao
AH
a) Biết
3
16 , .
4
AB
AC cm
AC
= =
Tính
,,
AB BC AH
,BH CH
b) Biết
1
14 , .
4
HB
AH cm
HC
= =
Tính
BC
Lời giải
a) Có
( )
3 33
.16 12
4 44
AB
AB AC cm
AC
=⇒= = =
Xét
ABC∆
vuông tại
A
, đường cao
AH
có
222
BC AB BC= +
(định lí pitago)
( )
2 22
12 16 400 20
BC BC cm⇒ =+= ⇒=
Hơn nữa lại có
2
.AB BH BC=
(hệ thức giữa cạnh và đường cao)
( )
22
: 12 : 20 7, 2BH AB BC cm⇒= = =
( )
20 7, 2 12,8HC BC BH cm=− =−=
Mặt khác
( )
2
. 7,2.12,8 92,16 9,6AH BH HC AH cm= = = ⇒=
Vậy
12 , 20 , 9,6 , 7,2 , 12,8AB cm BC cm AH cm BH cm HC cm
= = = = =
b) Ta có
( )
1
41
4
HB
CH BH
HC
=⇒=
Xét
ABC∆
vuông tại
A
, đường cao
AH
, có
2
.AH HB HC=
(2)
Từ (1)(2) suy ra
( )
2 222
4 . 14 4 49 7AH HB HB HB BH BH cm= ⇔= ⇒ =⇒ =
( )
4.7 28CH cm⇒==
Vậy
( )
7 28 35BC BH HC cm= + =+=
.
Bài 11:
Cho tam giác
ABC
vuông tại
A
, đường cao
AH
. Biết
5
26 ,
12
AB
BC cm
AC
= =
. Tính
,
AB AC
Và
,,AH BH CH
C
B
H
A
26
C
B
H
A
9
Lời giải
Cách 1: Từ giả thiết
22
5
12 5 12 25 144
AB AB AC AB AC
AC
=⇒=⇒ =
Áp dụng tính chất dãy tỉ số bằng nhau ta có
2 2 2 2 22
26
4
25 144 25 144 169 169
AB AC AB AC BC+
= = = = =
+
(
) (
)
2 10 , 24
5 12
AB AC
AB cm AC cm⇒ = =⇒= =
Xét
ABC∆
vuông tại
A
, đường cao
AH
, có
(
)
2 22
50
. : 10 : 26
13
AB BH BC BH AB BC cm
= ⇒= = =
( )
50 288
26
13 13
HC BC BH cm
⇒ = − =−=
Mặt khác
2
2
50 288 14400 120
..
13 13 13 13
AH BH CH AH= = = ⇒=
(cm)
Vậy
120 50 288
10 , 24 , , ,
13 13 13
AB cm AC cm AH cm BH cm HC cm= = = = =
Cách 2: Dùng phương pháp đại số
Từ giả thiết
5
12 5 12
AB AB AC
AC
=⇒=
Đặt
( )
0 5 , 12
5 12
AB AC
k k AB k AC k= = >⇒ = =
Xét
ABC∆
vuông tại
A
, có
222
BC AB AC= +
(định lí pitago)
Hay
( )
( ) ( )
22
22
26 5 12 4 2 0k k k kk= + ⇒ =⇒= >
Suy ra
10 , 24AB cm AC cm= =
.
Bài 12:
Cho
ABC∆
vuông tại
A
, đường cao
AH
. Biết
3
12 ,
4
AB
AH cm
AC
= =
. Tính
,,,,AB AC BC BH CH
Lời giải
C
B
H
A
10
Từ giả thiết
3
434
AB AB AC
AC
=⇒=
Đặt
( ) (
) ( )
0 3;4
34
AB AC
k k AB k cm AC k cm= = >⇒ = =
Xét
ABC∆
vuông tại
A
, đường cao
AH
có
( ) ( ) ( )
22
222 2 2
3 4 25 5
BC AB AC BC k k k BC k cm= + ⇒ = + = ⇒=
+
..AH BC AB AC=
(hẹ thức về cạnh và đường cao)
22
12.5 3 .4 60 12 12 60 0 5k kk k k k k k⇒ = ⇒ = ⇒ − =⇔=
Do đó
(
)
( ) ( )
3.5 15 ; 4.5 20 ; 5.5 25AB cm AC cm BC cm= = = = = =
Mặt khác
( )
22
2
15
.9
25
AB
AB BH BC BH cm
BC
= ⇒= ==
+
( )
25 9 16CH BC BH cm= − = −=
Vậy
( ) ( ) ( ) ( )
15 , 20 , 9 , 16AB cm AC cm BH cm CH cm= = = =
Bài 13:
Cho
ABC∆
vuông tại
A
, đường cao, phân
giác trong
AD
. Biết
75 , 100BD cm DC cm= =
.
Tính
,BH CH
Lời giải
Cách 1: Ta có
( )
75 100 175BC BD DC cm=+=+=
ABC∆
có
AD
là phân giác
BD AB
DC AC
⇒=
(tính chất đường phân giác)
22
75 3
100 4 3 4 9 16
AB AB AC AB AC
AC
⇒==⇒=⇒ =
Theo tính chất của dãy tỉ số bằng nhau, ta có:
222222
175
1225
9 16 25 25 25
AB AC AB AC BC+
= = = = =
( ) (
)
35 3.35 105 ; 4.35 140
34
AB AC
AB cm AC cm⇒ = =⇒= = = =
16
12
D
H
C
B
A
11
Xét
ABC∆
vuông tại
A
, đường cao
AH
có:
( )
2 22
. : 105 :175 63
AB BH BC BH AB BC cm= ⇒= = =
(
)
175 63 112CH BC BH cm= − = −=
Vậy
63 , 112
BH cm CH cm
= =
Cách 2:
ABC∆
có
AD
là phân giác
BD AB
DC AC
⇒=
(tính chất đường phân giác)
75 3
100 4
AB
AC
⇒==
Xét
ABC∆
vuông tại
A
, đường cao
AH
có:
2
2
2
2
2
.
. 99
. 16 16
.
AB BH BC
AB BH BC BH BH AB
BH CH
AC CH BC CH CH AC
AC CH BC
=

⇒ = =⇒ = =⇒=

=

(1)
Hơn nữa
(
)
75 100 175BC BD DC cm=+=+=
Do đó
( )
175BH CBC cm+=
(2)
Thay (1) vào (2) ta được
(
)
9 25
175 175 112
16 16
CH CH CH CH cm+=⇔ =⇔=
( )
175 112 63BH cm⇒ =−=
.
Bài 14:
Cho
ABC∆
vuông tại
A
, đường cao
( )
AH H BC∈
, biết
12 ; 16AB cm AC cm= =
, Phân
giác trong
AD
. Tính độ dài đoạn
HD
Lời giải
Xét
ABC∆
vuông tại
,
A
đường cao
(
)
AH H BC∈
, ta có:
222
()AB AC BC pytago+=
20( )BC cm⇒=
+) Áp dụng hệ thức lượng trong tam giác vuông ta có:
22
2
12
. 7,2( )
20
AB
AB BC BH BH cm
BC
= ⇒= ==
+) Ta có
AD
là phân giác của
BAC
3 20
()
43 47
DB AB BD DC
cm
DC AC
⇒==⇒==
16
12
D
H
C
B
A
12
20 60 60 36 552
.3 () ()
7 7 7 5 35
DB cm HD DB BH cm⇒ = = ⇒ = − =−=
.
Bài 15:
Cho
ABC∆
vuông tại
A
, có
6AB cm=
,
10 .BC cm=
Phân giác trong và ngoài tại đỉnh
B
cắt
AC
lần lượt tại
M
và
N
. Tính
BM
,
BN
Lời giải
Xét
ABC∆
vuông tại
A
, đường cao
AH
(
H BC∈
), ta có:
222
()AB AC BC pytago+=
8( )AC cm⇒=
+) Áp dụng tính chất đường phân giác trong tam giác, ta có:
63
1 3( )
10 5 3 5 8
AM AB AM MC AC
AM cm
MC BC
===⇒ ===⇒=
+) Áp dụng hệ thức lượng vào tam giác vuông
BMN
, ta có:
2
. 36 3. 12( ); 15( )AB AM AN AN AN cm MN AM AN cm= ⇒= ⇒ = = + =
22
. 15.3 3 5( ); . 15.12 6 5( )BM MN AM BM cm BN MN AN BN cm= =⇒ = = = ⇒=
.
Bài 16:
Tính diện tích tam giác có độ dài ba cạnh là
10 ,17 ,21cm cm cm
x
N
M
C
B
A
H
C
B
A
21
17
10
13
Lời giải
Xét
ABC∆
có
10 , 21 , 17AB cm BC cm CA cm= = =
Kẻ đường cao
11
. .21.
22
ABC
AH BC S AH BC AH⊥⇒ = =
Gọi
( )
( )
0
BH x cm x= >
thì
21HC x
= −
Áp dụng hệ pytago cho hai tam giác vuông
,ABH AHC
ta được:
( ) ( ) (
)
2
22222 2222
10 1 ; 17 21 2AH AB BH x AH AC CH x=−=− =−=−−
Từ (1)(2) suy ra:
( )
2
2 22
17 21 10 42 252 6x xx x− − = − ⇒ = ⇒=
Thay
6x =
vào (1) ta được:
( )( )
22
88 0
AH AH cm AH=⇔= >
Vậy
(
)
2
1
.21.8 84
2
ABC
S cm= =
.
BÀI TẬP TỰ LUYỆN
Bài 1:
Cho
ABC∆
vuông tại
A
, đường cao
AH
a) Biết
3, 4AB cm AC cm
= =
. Tính
,,BH CH AH
và
BC
b) Biết
9 , 16BH cm CH cm= =
.
Tính
,,,AB AC BC AH
Lời giải
a) Dùng định lí Pitago tính được
5BC cm=
Áp dụng hệ thức về cạnh và đường cao tính được
2,4 , 1,8 , 3,2AH cm BH cm CH cm= = =
b) Có
( )
9 16 25BC BH HC cm= + =+=
Áp dụng hệ thức về cạnh và đường cao ta tính được
15 , 20AH cm AC cm= =
C
B
H
A
14
Bài 2:
Cho
MNP∆
có
3, 4, 5MN cm NP cm MP cm= = =
a) Chứng minh tam giác
MNP
là tam giác
vuông
b) Tính đường cao
NK
c) Gọi
,IH
lần lượt là hình chiếu của
K
trên
,MN NP
. Tính
,IK HK
Lời giải
a) Dùng định lí Pitago đảo, chỉ ra
MNP∆
vuông tại
N
b)
MNP∆
vuông tại
N
, đường cao
NK
. Tính được
2, 4NK cm=
c) Tính được
1, 8 , 3, 2MK cm KP cm= =
MNK∆
vuông tại
K
, đường cao
KI
, tính được
1, 44KI cm=
NKP∆
vuông tại
K
, đường cao
KK
, tính được
1, 92KK cm=
.
Bài 3:
Cho
ABC
∆
vuông tại
A
, đường cao
AH
a) Biết
4
30 ,
3
AC
AB cm
AB
= =
.
Tính
,, ,,AC BC AH BH CH
b) Biết
9
6,
16
HB
AH cm
HC
= =
. Tính
BC
Lời giải
a)
( )
44
40
33
AC
AC AB cm
AB
=⇒= =
Áp dụng định lí pitago tính được
( )
50BC cm=
Áp dụng hệ thức về cạnh và đường cao, tính được
24 , 18 , 32AH cm BH cm CH cm= = =
b)
99
16 16
HB
HB HC
HC
=⇒=
Áp dụng hệ thức về cạnh và đường cao,
I
H
P
K
M
N
C
B
H
A
15
có
( )
22 2
9
. 6 . 64 8
16
AH HB HC HC HC HC HC cm= ⇒= ⇒ =⇒ =
( )
( )
4,5 12,5
HB cm BC cm⇒= ⇒=
.
Bài 4:
Cho
ABC∆
vuông tại
A
, có
6, 8AB cm AC cm
= =
. Các đườ
ng phân giác
trong và ngoài góc
B
cắt đường thẳng
AC
tại
D
và
E
. Tính
,
AD AE
Lời giải
Áp dụng định lí Pitago cho
ABC∆
vuông tại
A
, có
( )
222
10AB AC BC BC cm+ = ⇒=
Mặt khác
ABC
∆
có phân giác trong
63
10 5 3 5
AD AB AD DC
BD
DC BC
⇒===⇒=
Đặt
(
)
0 3; 5
35
AD DC
k k AD k DC k= = >⇒ = =
Mà
3 5 8 1 3, 5AD DC AC k k k AD cm DC cm+ = ⇒ + =⇒=⇒ = =
Hơn nữa
ABC∆
có phân giác ngoài
3
434
AE AB AE EC
BE
EC AC
⇒==⇒=
Đặt
( )
0 3, 4
34
AE EC
h h AE h EC h
= = >⇒ = =
Mà
( )
3 8 4 8 3.8 24AE AC EC h h h AE cm+ = ⇒ += ⇒=⇒ = =
.
E
D
C
B
A
16
Dạng 2: Tính chu vi, diện tích các hình
Cách giải:
Bước 1: Hình cần tính chu vi, diện tích là hình gì?
Bước 2: Viết công thức tính chu vi, diện tích của hình đó
Bước 3: Tính độ dài các đoạn thẳng chưa biết (đã học ở dạng 1)
Bước 4: Thay số và tính chu vi, diệc tích. Kết luận.
Bài 1:
Cho
ABC∆
vuông tại
A
, đường cao
(
)
AH H BC
∈
. Biết
9 , 16BH cm CH cm= =
. Tính
chu vi và diện tích của
ABC∆
Lời giải
Ta có
( )
9 16 25BC cm=+=
Áp dụng hệ thức và cạnh và đường cao cho
ABC∆
vuông tại
A
, đường cao
AH
, có:
( )
2
. 9.25 9.25 15AB BH BC AB cm= = ⇒= =
(
)
2
. 16.25 16.25 20AC CH BC AC cm= = ⇒= =
Chu vi của
ABC∆
là
( )
15 20 25 60AB BC CA cm+ + =++=
Diện tích của
ABC∆
là
( )
2
11
. .15.20 150
22
AB AC cm= =
Bài 2:
Cho
ABC∆
vuông tại
A
, đường cao
( )
AH H BC∈
. Biết
6 , 4,8AB cm AH cm= =
. Tính
chu vi và diện tích của
ABC∆
Lời giải
4,8
6
C
B
H
A
16
9
C
B
H
A
17
Cách 1: Vì
AH BC⊥
nên
0
90AHB =
Xét
ABH∆
vuông tại
H
, có
2 22
AB AH BH= +
(Định lí Pitago)
( )
3, 6BH cm⇒=
Xét
ABC∆
vuông tại
A
, đường cao
AH
, có
2
.AH BH BC=
(hệ thức giữa cạnh và đường cao)
( )
22
6
10
3, 6
AB
BC cm
BH
⇒= ==
Hơn nữa
222
AB AC BC+=
(Định lí Pitago)
(
)
2 2 2 22
10 6 64 8AC BC AB AC cm= − = −=⇒ =
Chu vi của
ABC∆
là
( )
6 8 10 24AB BC CA cm+ + =++ =
Diện tích của
ABC∆
là
(
)
2
11
. .6.8 24
22
AB AC cm= =
Cách 2:
Xét
ABC∆
vuông tại
A
, đường cao
AH
, có
( )
222 222
1 1 1 111
8
4,8 6
AC cm
AH AB AC AC
=+⇒=+⇒=
( )
2 2 2 22
10 6 8
AC BC AB AC cm⇒ = − = −⇒ =
Chu vi của
ABC
∆
là
( )
6 8 10 24AB BC CA cm+ + =++ =
Diện tích của
ABC∆
là
(
)
2
11
. .6.8 24
22
AB AC cm= =
Bài 3:
Cho
ABC∆
có
5, 7AC cm BC cm= =
a) Gọi
H
là hình chiếu của
A
trên
BC
và biết
4HC cm=
. Tính
AH
và diện tích
ABC
∆
b) Gọi
K
là hình chiếu của
H
trên
AC
. Tính
chu vi tứ giác
ABHK
Lời giải
a) Vì
H
là hình chiếu của
A
trên
BC
nên
AH BC⊥
tại
H
0
90AHB AHC⇒==
Xét
AHC
∆
vuông tại
H
có
( )
2 22
3AC AH HC AH cm= + ⇒=
7
5
B
H
C
K
A
18
( )
2
11
. .3.7 10,5
22
ABC
S AH BC cm= = =
b) Có
( )
743BH BC HC cm= − =−=
Xét
AHB∆
vuông tại
H
có
(
)
22 2
32AB AH BH AB cm= + ⇒=
Vì
K
là hình chiếu của
H
trên
AC
nên
HK AC⊥
tại
0
90K AKH CKH⇒==
Xét
AHC∆
vuông tại
H
, đường cao
HK
có
( )
2 22
. : 3 : 5 1, 8AH AK AC AK AH AC cm= ⇒= = =
( )
5 1, 8 3, 2KC AC AK cm⇒ = − =−=
Hơn nữa
( )
2
. 1,8.3,2 5,76 2,4HK AK KC HK cm= = = ⇒=
Vậy chu vi của tứ giác
ABHK
là
(
)
3 2 1,8 2,4 3 11, 443AB AK HK HB cm
+ + + = + + +≈
.
Bài 4:
Cho
ABC∆
vuông tại
C
, đường cao
CH
. Biết
15 , 16AC cm BH cm= =
. Tính diện tích
ABC∆
.
Lời giải
Đặt
( ) ( )
, 0 16AH x cm x AB x cm= >⇒ =+
Xét
ABC∆
vuông tại
C
, đường cao
CH
có
2
.AC AH AB=
(hệ thức về cạnh và đường cao)
(
) ( )
( )
2
15 16 9 25 0 9xx x x x⇒ = + ⇔ − + =⇔=
(thỏa mãn)
Vậy
( )
9 , 9 16 25AH cm AB cm
= =+=
Hơn nữa
( )
2
. 9.16 9.16 12CH AH HB CH cm= = ⇒= =
Diện tích
ABC∆
là
( )
2
11
. .12.25 150
22
CH AB cm= =
.
x
16
15
C
B
H
A
19
Bài 5:
Cho hình thang
(
)
//ABCD AB CD
, hai đường
chéo
AC
và
BD
vuông góc nhau tại
O
a) Chứng minh
1
.
2
ABCD
S AC BD
=
b) Biết
5,BD cm=
đường cao
4BH cm=
. Tính
diện tích hình thang
ABCD
Lời giải
a) Ta có
( )
111 1
.. .
222 2
ABCD ABD BDC
S S S AO BD CO BD BD AO CO BD CO=+= + = +=
b) Kẻ
( )
//BE AC E DC∈
mà
// , //AB CD E DC AB CE∈⇒
do đó tứ giác
ABEC
là hình bình hành (dấu hiệu nhận biết)
AC BE
⇒=
(tính chất hình bình hành)
Xét
BHD∆
vuông tại
H
có
2 22
BD BH HD= +
(Pitago)
(
)
22 2
54 3
HD HD cm⇒=+ ⇒ =
Vì
BD AC
⊥
và
//AC BE BD BE
⇒⊥
0
90DBE⇒=
Xét
DBE∆
vuông tại
B
, đường cao
BH
có
( )
22
16
. 4 3.
3
BH HD HE HE HE cm= ⇒= ⇒ =
(
)
(
)
2
16 16 400 20
. .3
3 39 3
BE HE HD HE BE cm

= + = + = ⇒=


Do đó
( )
20
3
AC cm=
. Vậy
( )
2
1 20 50
. .5
23 3
ABCD
S cm= =
.
Bài 6:
Cho
ABC∆
vuông tại
A
, đường cao
( )
AH H BC∈
, biết
20
; 420( )
21
AB
AH cm
AC
= =
,
Tính chu vi
?ABC∆
16
12
D
H
C
B
A
O
E
H
D
C
B
A
20
Lời giải
Ta có:
20
( 0) 20 ; 21
21 20 21
AB AB AC
k k AB k AC k
AC
= ⇒ = = >⇒ = =
Áp dụng hệ thức lượng trong tam giác vuông, ta có:
22 2
. . 420. 20.21. 420AH BC AB AC BC k k BC k= ⇒ = = ⇒=
Lại có:
222 2 2 2 2 2
2
29
400 441 841 (29 ) 29 29
BC k
BC AB AC k k k k k k k
BC k
=
= + = + = = ⇒ ⇒ = ⇔=
=
580( )
609( ) 2030( )
841( )
ABC
AB cm
AC cm P cm
BC cm
=
⇒ = ⇒=
=
BÀI TẬP TƯƠNG TỰ
Bài 1:
Cho
MNP∆
vuông tại
, 12 , 13
M MN cm NP cm
= =
, đường cao
MK
a) Tính
,,
MK MN KP
b) Tính diện tích
MNP
∆
Lời giải
a) Áp dụng định lí Pitago, tính được
(
)
5MP cm
=
Áp dụng hệ thức về cạnh và đường cao, tính được
( ) ( )
( )
60 144 25
,,
13 13 13
MK cm NK cm KP cm= = =
b)
( )
2
30
MNP
S cm
=
Bài 2:
Tính diện tích tam giác
ABC
có
10 , 17 , 21AB cm AC cm BC cm
= = =
13
12
N
K
P
M
10
17
B
C
H
A
21
Lời giải
Kẻ
AH BC
⊥
tại
H
vàv đặt
( )
,0BH x cm x= >
0
90AHB AHC⇒==
và
( )
21HC x cm= −
Hơn nữa
0
90
AHB AHC= =
Xét
AHB
∆
vuông tại
H
có
( )
2 22 222
1AB AH BH AH AB BH=+⇒=−
Xét
AHC∆
vuông tại
H
có
( )
2 22 222
2AC AH CH AH AC CH=+⇒=−
Từ (1)(2) suy ra
( )
2
2222222
10 17 21 6AB BH AC CH x x x−=−⇔−=−−⇔=
(thỏa mãn)
Vậy
( )
6BH cm=
Ta có
( )
2 2 2 22
10 6 64 8AH AB BH AH cm= − = −=⇒ =
Vậy
( )
2
11
. .8.21 84
22
ABC
S AH BC cm= = =
.
Bài 3:
Cho hình thang
ABCD
có
00
90 , 60AD B= = =
30 ,
CD cm CA CB= ⊥
. Tính diện tích hình thang
ABCD
Lời giải
a) Cách 1: Dùng phương pháp đại số hóa
Ta có
( )
0 00 0
90 90 60 30 1CAB ABC=− =−=
Hình thang
ABCD
có
( )
0
90 / / 2A D DC AB DCA CAB==⇒ ⇒=
Từ (1)(2) suy ra
0
30DCA =
Đặt
( )
,0AD x cm x= >
Xét
ADC∆
vuông tại
D
có
( )
0
1
30 2 2
2
DCA AD AC AC AD x cm=⇒= ⇒= =
Hơn nữa
( ) ( )
2
2 2 2 22 2
2 30 300 10 3AC AD DC x x x x AD cm= + ⇒ = + ⇒ = ⇒= =
y
x
30cm
B
C
A
D
60
0
22
( )
2 20 3AC x cm⇒==
Đặt
( )
,0BC y cm y= >
Xét
ABC∆
vuông tại
C
, có
( )
0
1
30 2 2
2
CAB BC AB AB BC y cm=⇒= ⇒= =
Lại có
(
)
( )
( )
2
2
2 2 2 22
2 20 3 400 20
AB AC BC y y y y BC cm
= + ⇒ = + ⇒ = ⇒= =
( )
2 40AB BC cm⇒= =
( )
( )
( )
2
. 30 40 .10 3
350 3
22
ABCD
AB CD AD
S cm
++
= = =
b) Cách 2: Chỉ ra
2AC AD=
Tính được
( )
10 3AD cm=
Kẻ
CH AB⊥
tại
H
Chỉ ra được
ADCH
là hình chữ nhật
( ) ( )
10 3 , 30CH AD cm HA CD cm⇒== ==
Hơn nữa
( ) ( )
2
2
. 10 40
CH
CH HA HB HB cm AB HA HB cm
HA
= ⇒= = ⇒=+=
Tính được
( )
2
350 3
ABCD
S cm=
.
23
Dạng 3: Chứng minh các hệ thức liên quan đến tam giác vuông
Cách giải: Sử dụng các hệ thức về cạnh và đường cao một cách hợp lý theo 3 bước:
Bước 1: Chọn các tam giác vuông thích hợp chứa các đoạn thẳng có trong hệ thức
Bước 2: Tính các đoạn thẳng đó nhờ hệ thức về cạnh và đường cao
Bước 3: Liên kết các giá trị trên để rút ra hệ thức cần chứng minh.
Bài 1:
Cho
ABC∆
vuông tại
A
, đường cao
AH
.
Chứng minh rằng:
a.
2222
AB CH AC BH+=+
b. Vẽ trung tuyến
AM
của
ABC∆
. Chứng
minh rằng:
+)
2
22 2
2
2
BC
AB AC AM+= +
+)
( )
22
2. .AC AB BC HM AC AB−= >
Lời giải
a) Xét tam giác vuông
HAB
và tam giác vuông
HAC
, theo định lý pytao ta có:
22 222
AB BH AH AC HC−= =−⇒
đpcm
b) Áp dụng định lý pytago vào tam giác vuông
ABC
, ta có:
2
2 2 22
222 2 2
;2 2
2 2 2 22
BC BC BC BC BC
AB AC BC AM BC

+= + =+ =+=


⇒
đpcm
Bài 2:
Cho hình bình hành
ABCD
có góc nhọn
A
.
Gọi
,IK
lần lượt là hình chiếu của
,BD
trên
đường chéo
AC
. Gọi
,MN
là hình chiếu của
C
trên các đường thẳng
,AB AD
. Chứng minh
rằng:
a.
AK IC=
H
M
C
B
A
K
I
N
M
D
C
B
A
24
b. Tứ giác
BIDK
là hình bình hành
c.
2
..AC AD AN AB AM
= +
Lời giải
a) Ta có:
;AK AI IK IC IK KC AK IC=+ =+⇒=
(đpcm)
b) Xét tứ giác BIDK, có:
//BI DK
BIDK
BI KD
⇒◊
=
là hình bình hành.
c) Ta có:
2
(.); (.) . .
AKD ANC g g ABI ACM g g AC AD AN AB AM∆ ∆ ∆ ∆ ⇒= +
##
(đpcm).
Bài 3:
Cho
2AB a=
cố định.
O
là trung điểm của
AB
, về cùng một phía của
AB
ta vẽ hai tia
,Ax By
, trong đó
,AB By AB Ax⊥⊥
. Lấy
điểm
C
thuộc
Ax
,
D
thuộc
By
sao cho
( )
0
90COD AC BD= ≤
. Hạ
OM
vuông góc
với
CD
, nối
OC
cắt
AM
tại
E
, nối
OD
cắt
BM
tại
F
.
a. Chứng minh
CO
và
DO
là phân giác của
;ACD BCD
b. Chứng minh tam giác
MAB
vuông tại
M
c. Chứng minh tứ giác
OEMF
là hình chữ
nhật
d.
..OE OC OF OD=
e. Cho
C
và
D
chuyển động mà
0
90COD =
. Chứng minh
.AC BD
không đổi
f. Cho
0
30MBA =
. Tính
AC
và
BD
theo
a
g. Xác định vị trí của
C
để cho:
3tanCDB =
Lời giải
a. Từ giả thiết suy ra
//AC BD
vì cùng
AB
⊥
I
f
2
1
H
2
1
O
M
C
D
B
A
25
Tứ giác
ABCD
là hình thang.
Gọi
I
là trung điểm của
CD OI
⇒
là đường trung bình của hình thang
ABCD
2
//
OI AC IOC C⇒ ⇒=
(so le trong)
Ta có
COD∆
vuông tại
O
(giả thiết)
12
IC ID IO IC IOC C C CO= ⇒ = ⇒= = = ⇒
là phân giác
ACD
Tương tự:
DO
là phân giác của góc
BDC
b) Theo tính chất đường phân giác
1
2
OM OA OB MO AB MAB⇒ = = ⇒ = ⇒∆
vuông tại
M
c)
OMC∆
vuông tại
M
và
OAC∆
vuông tại
A
, mà
12
CC=
(chứng minh trên)
( )
12
MOC AOC
C C OC AM E
OM OA cmt
=
=⇒ ⇒⊥ =
=
d) + e). Ta có:
02
90 . .
AO AC
AOC BOD AOC BDO AC BD AO BO a
BD BO
= = ⇒∆ ∆ ⇒ = ⇒ = =#
f) Ta có:
( )
0
1
/ / 30
OC MB AM O MBO⊥ ⇒= =
02
1
0. 30 . ; . 3
33
a
AC A tan a AC BD a BD a⇒= = = =⇒=
g) Hạ
,CH BD⊥
đặt
( )
0AC x x= >
Tứ giác
ACHD
là hình chữ nhật
;2
BH x CH AB a⇒= ==
Ta có
22
33
33 3
CH CH a a
tanCDB DH BD x
HD
=⇔ =⇔ = =⇒=+
Theo chứng minh trên:
2
.AC BD a=
22 2
22 22 2 2
2 2 10
. 2 . ( ) ( , 0)
3 3 39 9 3 9
10
33
a ax a a a a a
xx ax ax x a x xa
aa
x

 


( 10 1) ( 10 1)
33
aa
x AC


.
26
Bài 4:
Cho hình vuông
ABCD
, một điểm
E
bất kỳ
thuộc cạnh
AB
. Gọi
F
là giao điểm của
DE
Và
BC
. Chứng minh rằng:
22
11
DE DF
+
không đổi.
Lời giải
Dựng qua
D
đường thẳng vuông góc với
DE
cắt
BC
tại
P
Tam giác
DPF
, có:
222
111
CD DP DF
= +
, mà
CD DA=
;
12
DD=
(cùng phụ với
3
D
)
DAE DCP DE DP⇒∆=∆⇒=
Vậy
222
111
DE DF DA
+=
(đpcm).
Bài 5:
Cho tam giác nhọn
ABC
,
BD
và
CE
là hai
đường cao. Các điểm
,NM
trên các đường
thẳng
,BD CE
sao cho
0
90AMB ANC= =
.
Chứng minh rằng
AMN∆
cân.
Lời giải
Xét
ABD∆
và
ACE∆
có:
2
3
1
E
F
P
D
C
B
A
N
M
E
D
C
B
A
27
( )
0
: ; 90 . . 1
AB AD
BAD chung ADB AEC ABD ACE AE AB AD AC
AC AE
= = ⇒∆ ∆ ⇒ = ⇒ =#
AMB∆
vuông tại
M
(gt),
ME
là đường cao, theo hệ thức liên quan tới đường cao có:
(
)
2
.2
AM AE AB=
. Tương tự ta có:
( )
2
.3AN AD AC=
Từ (1)(2)(3) có:
22
AM AN AM AN AMN= ⇒ = ⇒∆
cân.
Bài 6:
Cho đoạn thẳng
4AB cm=
.
C
là điểm di động
sao cho
3.BC cm=
Vẽ tam giác
AMN
vuông
tại
A
có
AC
là đường cao. Xác định vị trí
điểm
C
để
22
11
AM AN
+
đạt giá trị lớn nhất.
Lời giải
Xét
AMN∆
vuông tại
A
,
AC
là đường cao (gt)
Theo hệ thức liên quan đường cao trong tam giác vuông, ta có:
222
111
AM AN AC
+=
Xét ba điểm
,,ABC
ta có:
( )
;1AC AB BC AC cm≥− ≥
Do vậy:
2
11
11
AC AC
≤⇔ ≤
, dấu “=” xảy ra khi và chỉ khi
C
nằm giữa A và B
Vậy khi
C
nằm giữa A và B sao cho
3BC cm=
thì
22
11
AM AN
+
đạt giá trị lớn nhất.
B
N
A
C
M
28
Bài 7:
Cho
ABC∆
có ba cạnh tỉ lệ với
3, 4, 5
và chu vi tam giác đó là
( )
48 cm
. Chứng minh rằng
ABC∆
vuông
Lời giải
Gọi
,,abc
là độ dài ba cạnh của
ABC
∆
Theo đề bài ta có:
345
48
abc
abc
= =
++=
Ta có:
48
4 12; 16; 20
3 4 5 12 12
a b c abc
abc
++
=== = =⇐= = =
Lại có:
( )
( )
22 2 2
2 22
22
12 16 400 1
20 400 2
ab
c a b ABC
c
+= + =
⇒ = + ⇒∆
= =
vuông.
Bài 8:
Cho
ABC∆
cân tại
A
( )
0
90A <
, kẻ
BM CA⊥
.
Chứng minh rằng:
2
21
AM AB
MC AC

= −


Lời giải
Lấy
E
đối xứng với
C
qua
A
thì
BCE∆
vuông tại
B
Áp dụng hệ thức về cạnh
2
' '.b ba=
ta được:
( )
22
2
.1
2
BC BC
BC MC ME MC
CE AC
= ⇒= =
Mặt khác
( )
2 22
2
2
22
BC AC BC
AM AC CM AC
AC AC
−
=−=− =
Chia (1) cho (2) theo từng vế ta được:
2
22
2
2
21
AM AC BC AC
MC BC BC
−

= = −


(đpcm).
E
B
C
M
A
29
Bài 9:
Cho
ABC∆
vuông tại
A
với đường cao
AH
.
Trên nửa mặt phẳng bờ
BC
có chứa điểm
A
lấy điểm
D
sao cho
.
2
AB
DB DC
= =
Chứng
minh rằng
,BD DH
và
HA
là độ dài ba cạnh
của một tam giác vuông.
Lời giải
Gọi
O
là trung điểm của
BC
Đặt
0OB OC R= = >
, do
(
)
2
AB
DB DC gt DO
R
= = ⇒
là đường trung trực của đoạn
BC
hay
DOC∆
vuông tại
.O
Gọi
;2HC x OH RR x BH R x=⇒=− =−
Áp dụng hệ thức pytago vào
DOC∆
và
DOH∆
vuông tại
,O
ta được:
( ) ( ) ( ) ( )
22
22222 2 22 2 2 2
2; 3DC OC DO R DO DH DO OH DO R x DO DH R x= + =+ = + = +− ⇒ = −−
Thế (3) vào (2) ta được:
(
)
2 2 22 2 2 2
24DC R DH R Rx x DH AH
= + −+ −= +
Lại có
2 22
,,DC DB BD DH AH BD DH HA=⇒= +⇒
là độ dài ba cạnh của một tam giác vuông
(theo định lý Pytago đảo).
Bài 10:
Cho hình vuông
ABCD
. Gọi
I
là một điểm
nằm giữa
A
và
B
. Tia
DI
và tia
CB
cắt nhau
ở
K
. Kẻ đường thẳng qua
D
, vuông góc với
DI
. Đường thẳng này cắt đường thẳng
BC
tại
L
. Chứng minh rằng
a) Tam giác
DIL
là tam giác cân
b) Tổng
22
11
DI DK
+
không đổi khi
I
thay đổi
H
O
D
B
C
A
D
L
C
I
K
B
A
3
2
1
30
trên cạnh
AB
.
Lời giải
a) Tứ giác
ABCD
là hình vuông (giả thiết)
AD CD⇒=
và
0
90
ADC DCB
= =
(tính chất hình vuông)
Lại có
00
180 90DCL DCB DCL
+=⇒=
Mặt khác
( )
0
0
12 32 31
90 ; 90
D D ADC D D IDL DL DI D D+= = += = ⊥ ⇒=
(phụ
2
D
)
Xét
ADI∆
và
CDL∆
, có
( )
0
13
90DAI DCL
AD DC ADI CDL gcg DI DL DIL
DD
= =
= ⇒∆ =∆ ⇒ = ⇒∆
=
cân tại
D
b) Xét
DKL∆
vuông tại
D
, đường cao
DC
có
222
11 1
DL DK DC
+=
(hệ thức cạnh và đường cao)
mà
222
11 1
DI DL
DI DK DC
=⇒+ =
hơn nữa
DC
là cạnh hình vuông
ABCD
nên
DC
không đổi
Vậy
22
11
DI DK
+
không đổi khi
I
thay đổi trên cạnh
AB
.
Bài 11:
Cho
MNE∆
. Từ một điểm
O
bất kỳ nằm trong
tam giác kẻ
,,OA OB OC
lần lượ
t vuông góc
với
,MN NE EM<
(
A
thuộc
MN
,
B
thuộc
NE
,
C
thuộc
EM
). Chứng minh rằng
222 22 2
MA NB EC AN BE CM++= ++
Lời giải
Ta có
OA MN⊥
tại
A
⇒
0
90OAM OAN
= =
OB NE
⊥
tại
0
90B OBN OBE⇒==
;
OC ME⊥
tại
0
90
B OCE OCM⇒= =
Áp dụng định lí Pitago cho các tam giác vuông
,,,,OAM OBN OBE OCE OCM∆ ∆∆∆∆
, có:
( )
2 22 2 2
1MO MA OA MC OC
=+= +
;
( )
2222 2
2NO OB NB OA AN=+=+
( )
2 2 2 22
3EO OC EC OB BE=+=+
O
A
N
B
E
C
M
31
Cộng (1)(2)(3) theo vế ta được:
222 2 2 2 2 22 222
MA OA OB NB OC EC MC OC OA AN OB BE++++ + = + ++ ++
2 22 2 2 2
MA NB EC AN BE CM⇒ ++= ++
(đpcm).
Bài 12:
Cho
ABC∆
vuông tại
A
, đường cao
AH
. Gọi
,MN
lần lượt là hình chiếu của
H
trên
,AB AC
. Chứng minh rằng
a)
..AM AB AN AC=
b)
2
HB AB
HC AC

=


c)
. ..HB HC MA MB NA NC
= +
Lời giải
a) Ta có
AH
là đường cao của
ABC∆
AH BC
⇒⊥
tại
H ⇒
0
90
AHB AHC= =
Có
,MN
lần lượt là hình chiếu của
H
trên
,,AB AC HM AB HN AC⇒⊥ ⊥
tại
N
Xét
AHB∆
vuông tại
H
, đường cao
HM
có
2
.
AH AM AB=
(1)
Xét
AHC∆
vuông tại
H
, đường cao
HN
có
2
.AH AN AC
=
(2)
Từ (1)(2) suy ra
..AM AB AN AC=
b) Xét
ABC∆
vuông tại
A
, đường cao
AH
có
2
22
2
.
.; .
.
AB BH BC BH
AB BH BC AC CH CB
AC CH CB CH
= = ⇒= =
hay
2
HB AB
HC AC

=


c) Xét
AHB∆
vuông tại
H
đường cao
HM
có
2
.HM MA MB=
(3)
Xét
AHC∆
vuông tại
H
đường cao
HN
có
2
.HM MA MB
=
(4)
Từ (3)(4)
22
..MA MB NA NC HM HN⇒+=+
(5)
MHN∆
vuông tại
22 2
H HM HN MN⇒ +=
(6)
Từ (5)(6)
2
..MA MB NA NC MN⇒+=
(7)
Tứ giác
AMHN
có
0
90AMH ANH MAN AMNH= = = ⇒◊
là hình chữ nhật
AH MN⇒=
(8)
Xét
ABC
∆
vuông tại
A
, đường cao
AH
có:
2
.AH HB HC=
(9)
M
N
C
H
B
A
32
Từ (7)(8)(9) suy ra
. ..
HB HC MA MB NA NC
= +
.
Bài 13:
Cho tứ giác
ABCD
có
0
90CD+=
. Chứng
minh rằng
22 22
AB CD AC BD
+=+
Lời giải
Vì
00
90 180CD+= <
nên hai đường thẳng
AD
và
BC
cắt nhau
Gọi
E
là giao điểm của
AD
và
BC
Xét
DCE
∆
có
00
90 90C D DCE+= ⇒ =
Áp dụng định lí Pitago ta có:
ABE∆
vuông tại
2 22
E AB AE BE⇒=+
DCE∆
vuông tại
2 22
E DC DE CE⇒=+
ACE∆
vuông tại
2 22
E AC AE CE⇒=+
ABD∆
vuông tại
2 22
E BD DE BE⇒=+
Do đó
( ) (
) ( ) (
)
22 22 22 22 2 2 22
AB CD AE BE DE CE AE CE BE DE AC BD+=+++=+++ =+
.
Bài 14:
Cho hình chữ nhật
ABCD
có
2AB AD=
. Trên
cạnh lấy điểm
E
bất kì. Tia
AE
cắt đường
thẳng
CD
tại
F
Chứng minh rằng
22 2
11 1
4AB AE AF
= +
Lời giải
x
H
D
C
F
E
B
A
A
D
C
B
E
33
Kẻ tia
Ax AF
⊥
tại
A
, cắt đường thẳng
CD
tại
H
Xét
AHF∆
vuông tại
A
, đường cao
AD
có
2 22
111
AD AH AF
= +
(1)
Chỉ ra
HAD EAB
=
(phụ với
DAE
) dẫn đến
(
)
ADH ABE gg
∆∆∽
( )
( )
1 11
2 ;2
2 22
AH AD
AB AD AH AE AD AB
AE AB
⇒ == = ⇒= =
Từ (1)(2)
22
2 2 22 22 2
1 1 1 441 11 1
4
11
22
AF AB AH AF AB AE AF
AB AH
⇒ = +⇔= +⇒=+



.
Bài 15:
Cho hình thoi
ABCD
có
0
120A =
. Tia
Ax
tạo
với góc
BAx
bằng
0
15
và cắt cạnh
BC
tại
M
,
cắt đường thẳng
DC
tại
N
. Chứng minh rằng
22 2
11 4
3AM AN AB
+=
.
Lời giải
Trên cạnh
DC
lấy điểm
E
sao cho
0
15DAE =
( )
0
90EAN BAD DAE BAx⇒=− +=
Kẻ
AH DC⊥
tại
H
Xét
AEN∆
vuông tại
A
, đường cao
( )
22 2
11 1
1AH
AE AN AH
⇒+=
( )
DAE BAM gcg AE AM∆ =∆ ⇒=
(2)
ADC∆
có
0
60ADC DAC ADC= = ⇒∆
đều
ADH∆
vuông tại
2
2 22 2222 2 2
33
24 4
AD
H AD AH DH AH AD DH AD AD AB

⇒=+⇒=−=− = =


( )
22
14
3
3AH AB
⇒=
N
B
M
C
H
E
D
A
34
Từ (1)(2)(3) suy ra
22 2
11 4
.
3AM AN AB
+=
35
BÀI TẬP TRẮC NGHIỆM
Câu 1: Cho
ABC∆
vuông tại
A
, đường cao
AH
, có
( ) ( )
9 , 12 .AB cm AC cm= =
Độ dài ba cạnh
,,AB BH CH
lần lượt là:
a)
( )
9,6 cm
b)
( )
6,9 cm
c)
(
)
8, 6
cm
d)
( )
6,8 cm
Chọn đáp án A
Giải thích: Ta có:
Áp dụng định lí Pytago vào tam giác
ABC
vuông tại
A
, ta có:
22 2
BC AB AC= +
( )
22
9 12 225 15BC cm=+= ⇒=
Áp dụng hệ thức lượng trong tam giác vuông
ta có:
( )
22
81
. 9 15 5, 4
15
AB BC BH BH BH cm= ⇔= ⇒ ==
Ta có:
( )
15 5, 4 9, 6
CH BC BH cm=− =−=
.
Câu 2: Cho
OEF∆
vuông tại
O
, đường cao
OI
, có
( )
( )
3,12
IE cm FI cm= =
. Độ dài đoạn thẳng
,OE OF
lần lượt là:
a)
35
b)
45
c)
55
d)
65
Chọn đáp án D
Giải thích: Ta có:
Áp dụng hệ thức lượng trong tam giác vuông
OEF
vuông tại
O
, đường cao
OI
, ta có:
( )
( )
2
. 3 12 .3 45 45 3 5
OE EF EI OE cm
= =+ =⇒= =
(
)
2
. 3 12 .12 180
OF EF FI==+=
( )
180 6 5OF cm⇒= =
Vậy
( )
( )
35 ; 65 .OE cm OF cm= =
12
3
F
E
I
O
12
9
C
B
H
A
36
Câu 3: Cho
ABC∆
vuông tại
A
, đường cao
AI
, có
(
) (
)
13 , 12
AB cm AI cm
= =
. Diện tích tam
giác
ABC
bằng?
a)
(
)
2
202,6
cm
b)
( )
2
202,7 cm
c)
(
)
2
202,8
cm
d)
(
)
2
202,9
cm
Chọn đáp án C
Giải thích: Ta có:
Áp dụng định lí Pytago vào
ABI∆
vuông tại
I
, ta có:
2 22 2 22
AB AI BI BI AB AI=+⇒= −
( )
22
13 12 25 5 .BI cm
=−⇒= =
Theo hệ thức lượng trong tam giác vuông, ta
có:
( )
22
2
2
13
. 33,8
5
AB
AB BC BI BC cm
BI
= ⇔= ==
(
)
2
11
. .12.33,8 202,8
22
ABC
S AI BI cm= = =
Câu 4: Cho
ABC∆
vuông tại
A
, đường cao
AH
, có
(
)
1
5
2
AB AC cm= =
. Độ dài đường cao
AH
bằng
a)
5
b)
25
c)
35
d)
45
Chọn đáp án B
Giải thích: Ta có:
Ta có:
( )
1
5 10
2
AB AC AC cm= =⇒=
Áp dụng định lí Pytago vào tam giác vuông
ABC
, ta có:
2 2 22 2
5 10 125BC AB AC= + =+=
( )
125 5 5BC cm⇒= =
Tam giác
ABC
, vuông tại
,A
có đường cao
..
AH AH BC AB AC⇒=
C
B
H
A
12
13
C
B
I
A
37
(
)
. 5.10
25
25
AB AC
AH cm
BC
⇒= = =
.
Câu 5: Cho
ABC∆
vuông tại
A
, biết
2
, 2 13.
3
AB
BC
AC
= =
Độ dài đường cao
AH
của
ABC∆
bằng bao nhiêu?
a)
0,3
b)
3, 3
c)
3, 33
d)
3, 03
Chọn đáp án C
Giải thích: Ta có:
( )
( )
22
2 22
24 4
12
3 9 13
AB AB AB
AC AC AB AC
=⇒=⇔ =
+
Mà
( )
2
222
2 13 52AB AC BC+== =
Từ (2), suy ra:
( )
2
2
4
16 4
52 13
AB
AB AB cm=⇒ =⇒=
Từ (1), suy ra:
( )
42
6
3
AC cm
AC
=⇔=
Ta có:
. 12
. . 3, 33
13
AB AC
AH BC AB AC AH
BC
= ⇔= = ≈
Câu 6: Cho
ABC∆
vuông tại
A
, có
( )
( )
18 , 24AB cm AC cm= =
. Các đường phân giác trong và
ngoài của góc
B
cắt đường thẳng
AC
lần lượt tại
,
MN
. Tính độ dài đoạn
MN
a)
6
b)
7
c)
8
d)
9
Chọn đáp án D
Giải thích: Ta có:
Xét
ABC∆
vuông tại
A
, ta có:
2 2 222
18 24 900BC AB AC= + =+=
( )
900 30BC cm⇒= =
Do
BM
là đường phân giác của
ABC
24
18
N
M
C
A
B
C
B
H
A
38
18 3
30 5
AM AB
MC BC
⇒===
33
9
3 5 24 8
AC
AM AM
AM
AM MC
⇒ = ⇔ =⇒=
++

Câu 7: Hình thang
ABCD
có
// ,AB CD
hai đường chéo vuông góc. Diện tích hình thang bằng
bao nhiêu biết
15
BD cm=
, đường cao hình thang bằng
( )
12
cm
.
a)
( )
2
150 cm
b)
( )
2
250 cm
c)
( )
2
105 cm
d)
( )
2
205 cm
Chọn đáp án A
Giải thích: Ta có:
Kẻ
2 2 2 22
15 12 81
BH CD DH BD BH⊥⇒ = − =−=
( )
22
15 12 81 9DH cm=−=⇒ =
Qua
B
kẻ đường thẳng song song với
AC
,
đường thẳng này cắt
DC
ở
E
Xét tam giác
DBE
vuông tại
B
, có:
2
22
15
. 15 9. 25
9
BD DH DE DE DE= ⇒= ⇔ = =
Diện tích hình thang
ABCD
là:
( )
( )
2
.
.
150
22
ABCD
AB CD BH
DE BH
S cm
+
= = =
.
Câu 8: Tam giác
MON
vuông tại
O
, đường phân giác của
O
cắt cạnh huyền
MN
thành hai
đoạn có đồ dài
( )
45
7
cm
và
( )
60
7
cm
. Diện tích của
MON∆
bằng bao nhiêu
a)
( )
2
52 cm
b)
( )
2
53 cm
c)
( )
2
54 cm
d)
( )
2
55 cm
H
E
D
C
B
A
39
Chọn đáp án C
Giải thích: Ta có:
Gọi
I
là giao điểm của tia phân giác của góc
O
và cạnh
MN
, ta có:
( )
2
2
45
45 3 9
7
1
60
60 4 16
7
OM IM OM
ON IN ON
====⇒=
( )
2
2
22
93
2
9 16 5
MN
OM OM
OM ON ON
⇒ = ⇒=
++

Ta có:
(
)
45 60
15
77
MN MI IN cm=+=+=
Từ (2), suy ra:
( )
3. 3.15
9
55
MN
OM cm= = =
Từ (1), suy ra:
( )
4. 4.9
12
33
OM
ON cm= = =
Do đó
( )
2
11
. .9.12 54
22
OMN
S OM ON cm= = =
.
Câu 9: Tam giác
ABC
vuông tại
A
, đường cao
AH
. Khẳng định nào sau đây đúng
a)
AHB CAB∆∆
#
b)
AHC BAC∆∆#
c)
AHB CHA∆∆#
d) Cả
,,ABC
đều đúng
Chọn đáp án D
Giải thích: Ta có:
a)
( )
AHB CAB gg
∆∆#
b)
(
)
AHC BAC gg∆∆#
c)
( )
AHB CHA CAB∆∆ ∆##
Câu 10: Tam giác
MNP
vuông tại
M
, đường cao
MH
. Khẳng định nào sau đây sai
a)
22
.; .MN NP NH MP NP PH= =
b)
2
.; . .MH HN HP MN MP NP MH
= =
c)
2 22
1 11
NH MN MP
= +
d)
,AB
đúng,
C
sai
O
I
M
N
C
B
H
A
40
Chọn đáp án D
Giải thích: Ta có:
a)
22
.; .MN NP NH MP NP PH= =
b)
2
.; . .
MH HN HP MN MP NP MH= =
c)
2 22
1 11
MH MN MP
= +
P
N
H
M
41
BÀI TẬP VỀ NHÀ
Bài 1:
Cho
ABC∆
vuông tại
A
, đường cao
AH
.
a. Biết
6 , 4,5 .AH cm BH cm= =
Tính
,AB AC
,
,
BC HC
b. Biết
6, 3AB cm BH cm= =
. Tính
AH
và tính
chu vi của các tam giác vuông trong hình vẽ
Hướng dẫn giải
a) Tính được:
7,5, 10, 12,5, 8AB cm AC cm BC cm HC cm 
b)
33 , 18 63 , 9 33 ; 9 93
ABC ABH ACH
AH cm P cm P cm P cm  
Bài 2:
Cho
ABC∆
vuông tại
A
, đường cao
AH
.
Tính diện tích
ABC∆
, biết
12AH cm=
9BH cm=
Hướng dẫn giải
Ta tính được:
2
150
ABC
S cm
Bài 3:
Cho hình thang
ABC∆
vuông tại
A
và
D
.
Cho biết
15 , 20
AB cm AD cm= =
, các đường
chéo
AC
và
BD
vuông góc với nhau tại
O
.
Tính
a. Độ dài các đoạn thẳng
OB
và
OD
b. Độ dài đoạng thẳng
AC
c. Diện tích hình thang
ABCD
Hướng dẫn giải
H
C
B
A
H
C
B
A
20
15
D
C
B
A
42
a) Áp dụng các hệ thức lượng trong tam giác vuông
ABD
, tính được:
2,5, 9, 16BD cm OB cm OD cm 
b) Áp dụng các hệ thức lượng trong tam giác vuông
DAC
tính được:
( )
100
12 ;
3
OA cm AC cm= =
c) Tính được:
( )
2
1250
3
ABCD
S cm
=
Bài 4:
Cho hình chữ nhật
ABCD
có
8AB cm=
15BC cm=
a. Tính độ dài đoạn thẳng
BD
b. Vẽ
AH
vuông góc
BD
tại
H
. Tính độ dài
đoạn thẳng
AH
c. Đường thẳng
AH
cắt
BC
và
DC
lần lượt
tại
I
và
K
. Chứng minh
2
.AH HI HK
=
Hướng dẫn giải
a)
17
BD cm
b)
120
17
AH cm
K
I
H
D
C
B
A
43
Bài 5:
Cho tam giác
ABC
vuông tại
A
. Đường cao
AH
, kẻ
,
EH HF
lần lượt vuông góc với
,AB AC
. Chứng minh rằng:
a.
3
EB AB
FC AC


b.
3
..BC BE CF AH
Hướng dẫn giải
a) Sử dụng hệ thức giữa cạnh góc vuông với hình chiếu của nó lên cạnh huyền và cạnh huyền
trong các tam giác vuông HBA và HCA
b) Áp dụng hệ thức giữa đường cao và hình chiếu cạnh góc vuông lên cạnh huyền trong tam
giác vuông ABC
Bài 6:
Cho tam giác
ABC
cân tại
A
có
,
AH BK
là
hai đường cao. Kẻ đường thẳ
ng vuông góc
BC
tại
B
cắt tia
CA
tại
D
a.
2BD AH
b.
22 2
111
4BK BC HA

Hướng dẫn giải
a) Chứng minh
AH
là đường trung bình của
BCD∆
b) Sử dụng hệ thức giữa đường cao và các cạnh góc vuông trong tam giác vuông
BCD
và áp
dụng câu a
H
C
B
A
D
K
H
C
B
A
| 1/43
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

ÔN TẬP HỆ THỨC VỀ CẠNH VÀ ĐƯỜNG CAO TRONG TRONG TAM GIÁC VUÔNG A. Tóm tắt lý thuyết
Khi giải các bài toán liên quan đến cạnh và đường cao trong tam giác vuông, ngoài việc nắm
vững các kiến thức về định lý Talet, về các trường hợp đồng dạng của tam giác, cần phải nắm
vững các kiến thức sau:
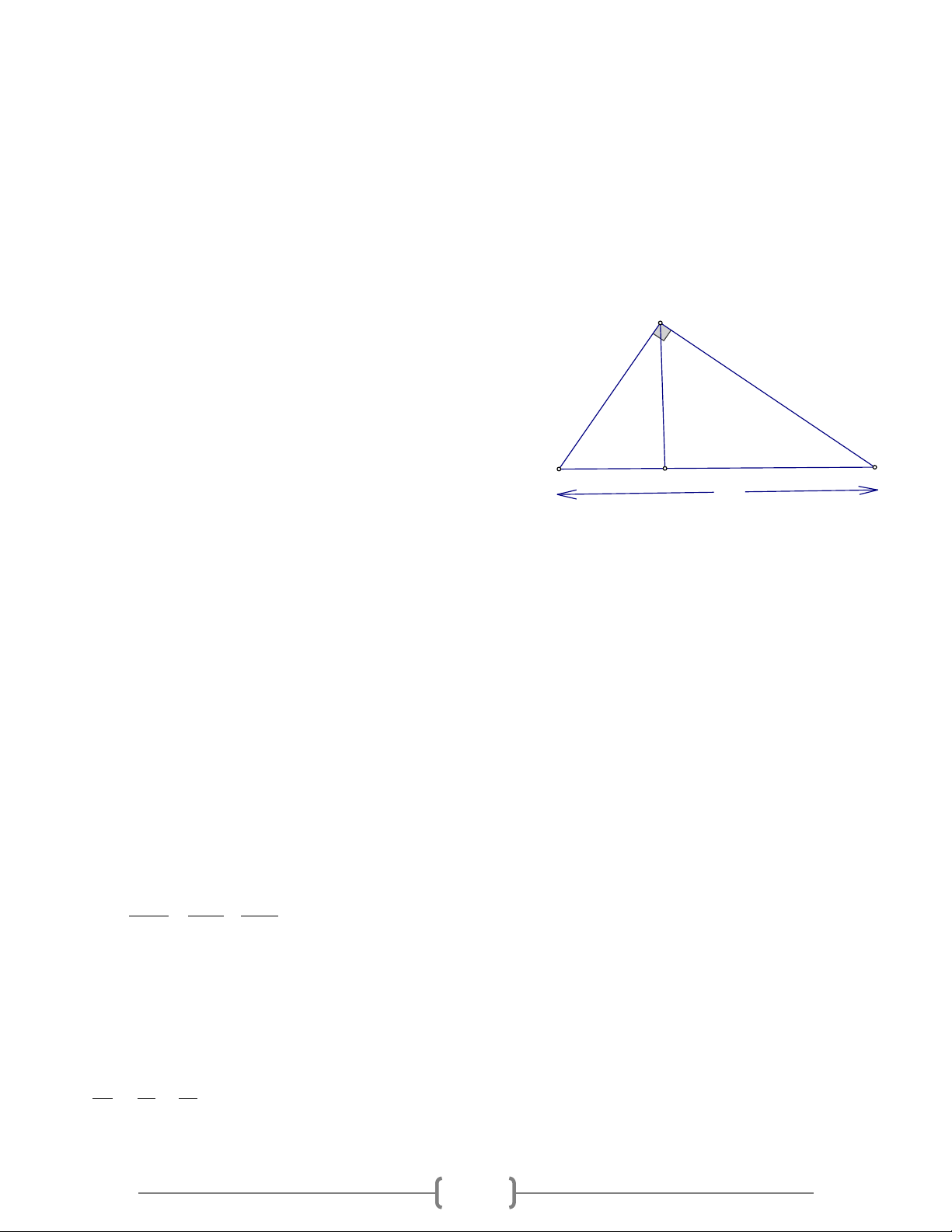
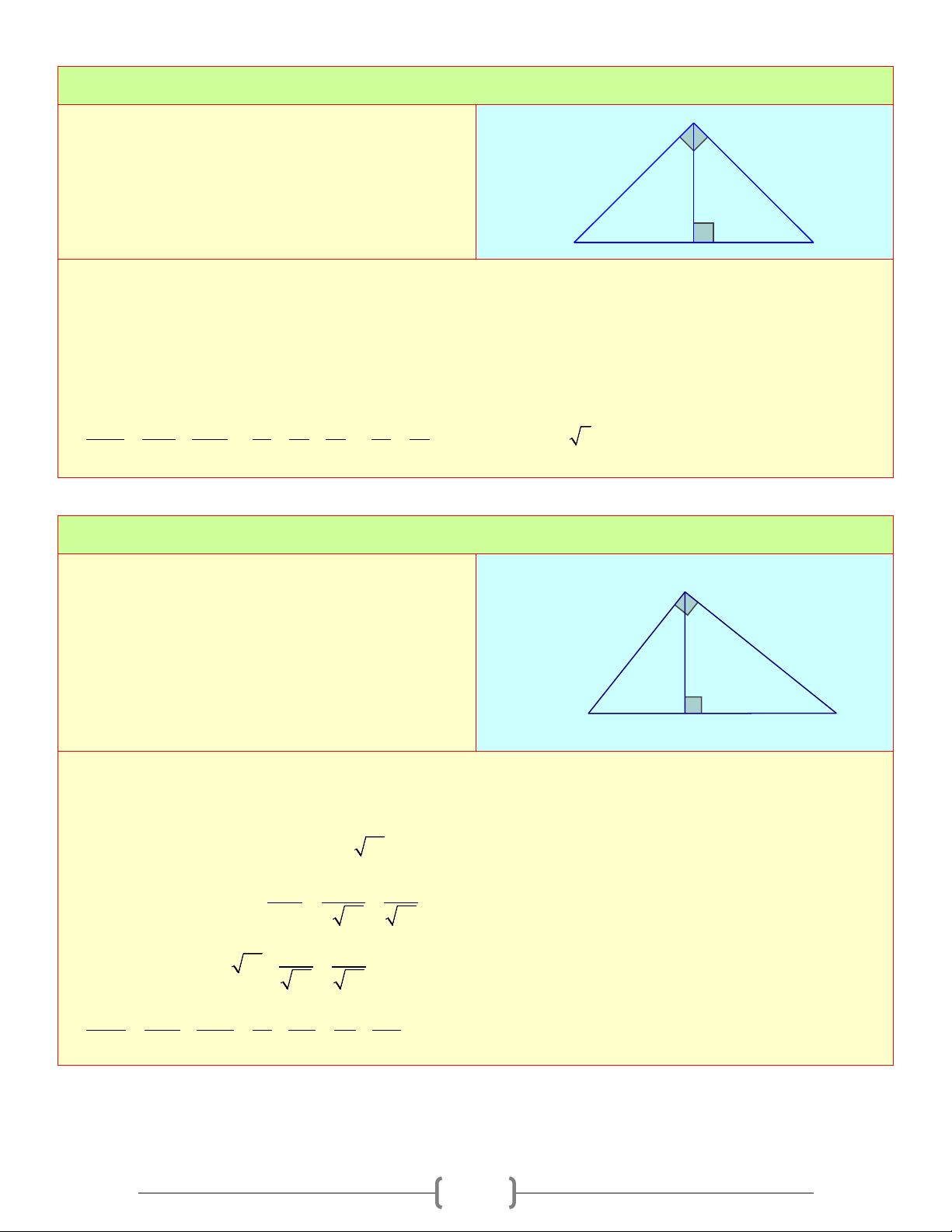
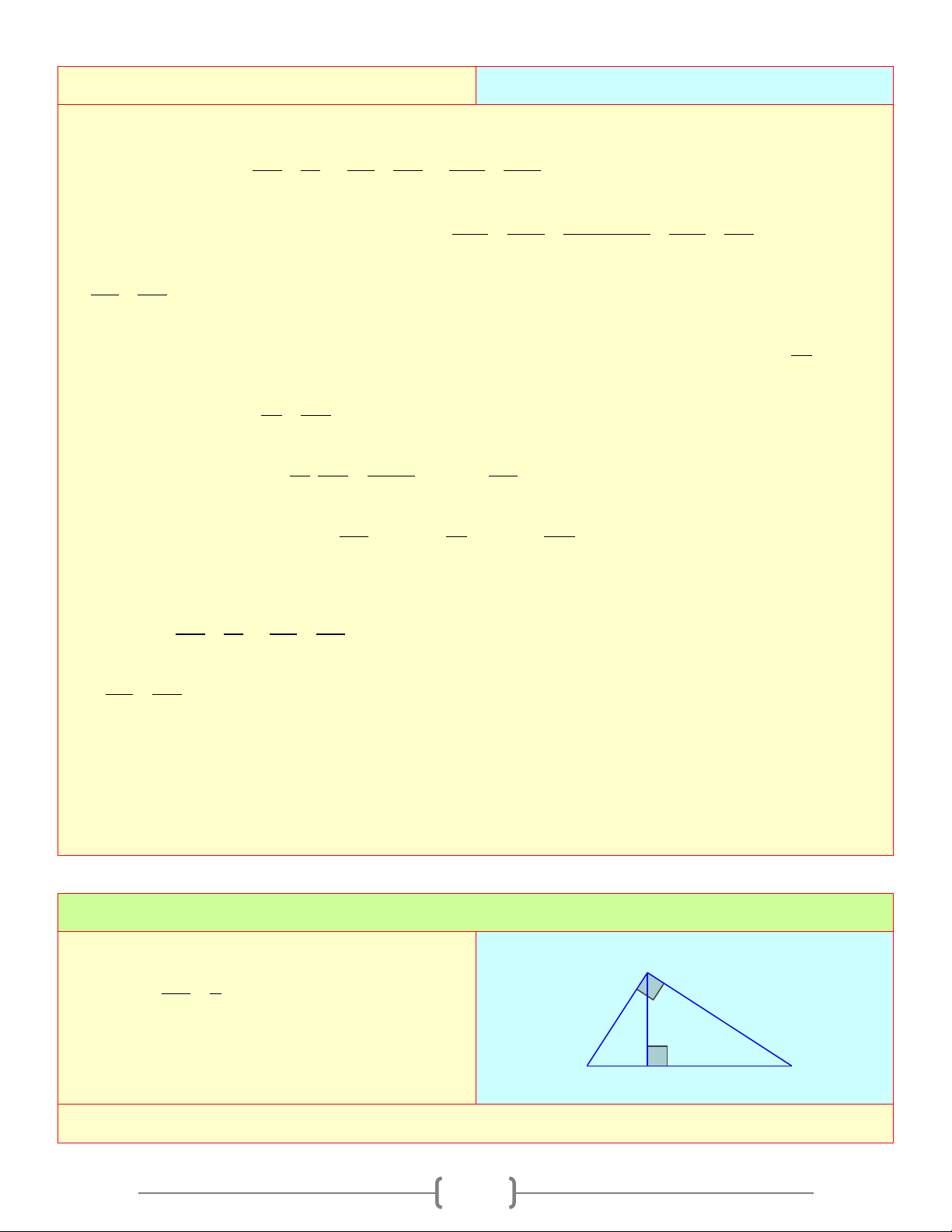
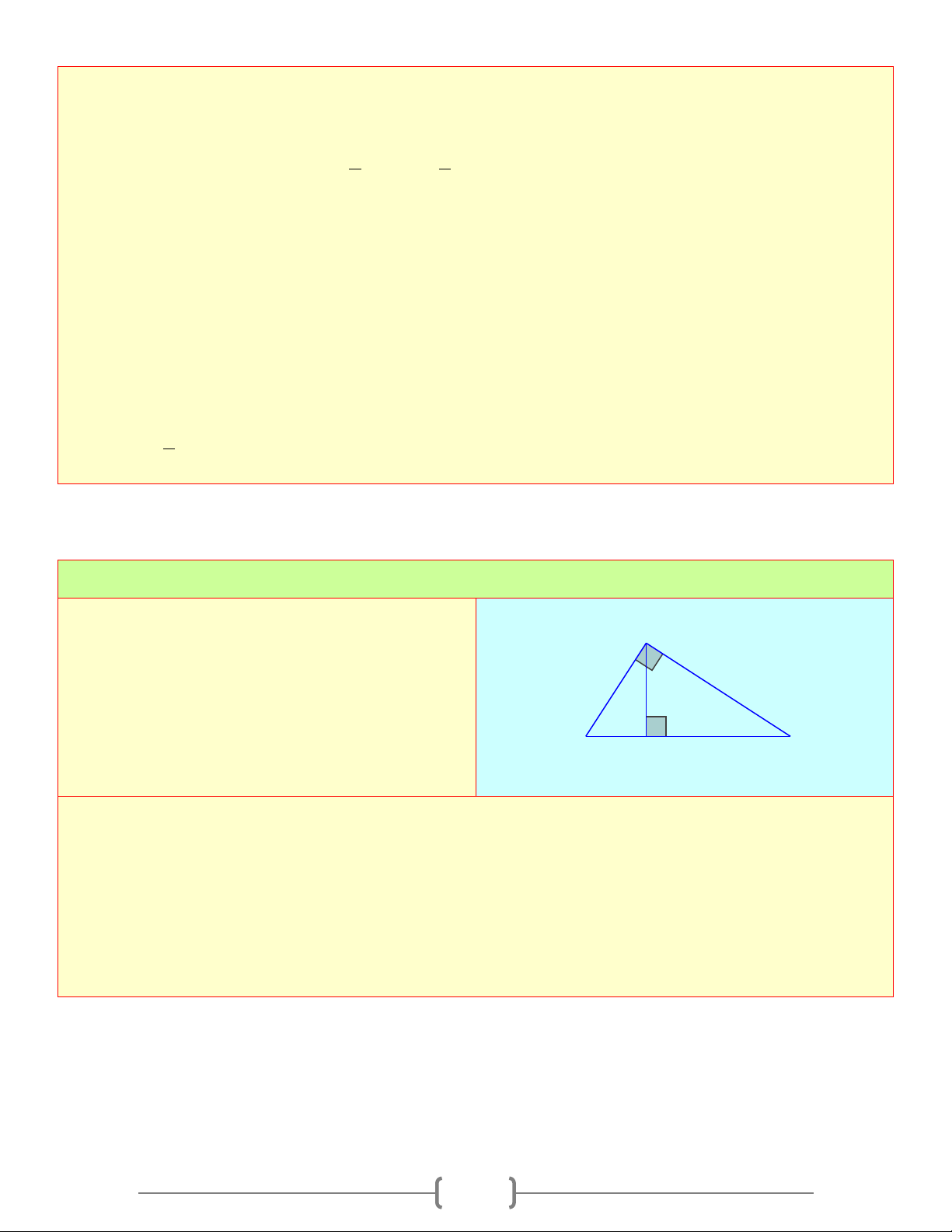
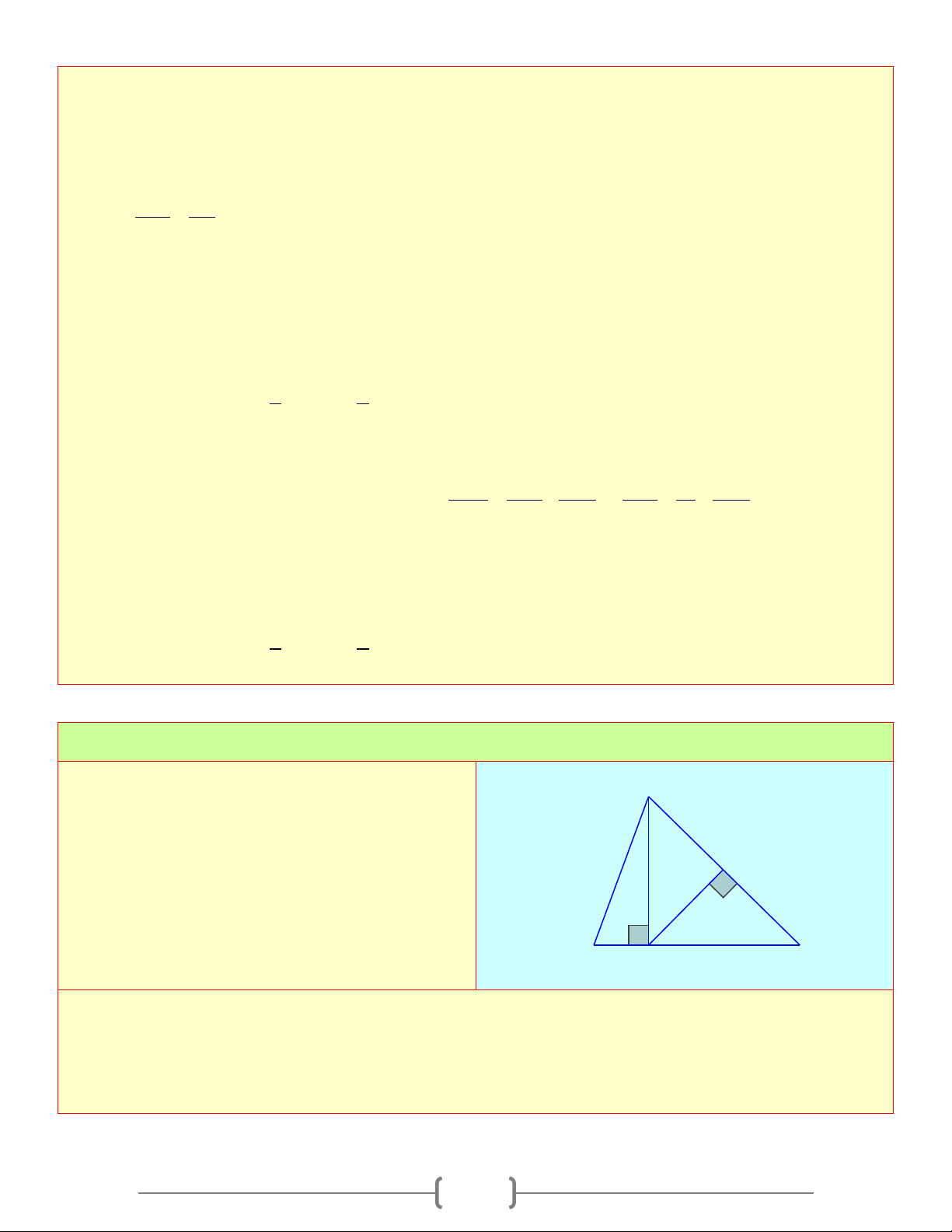
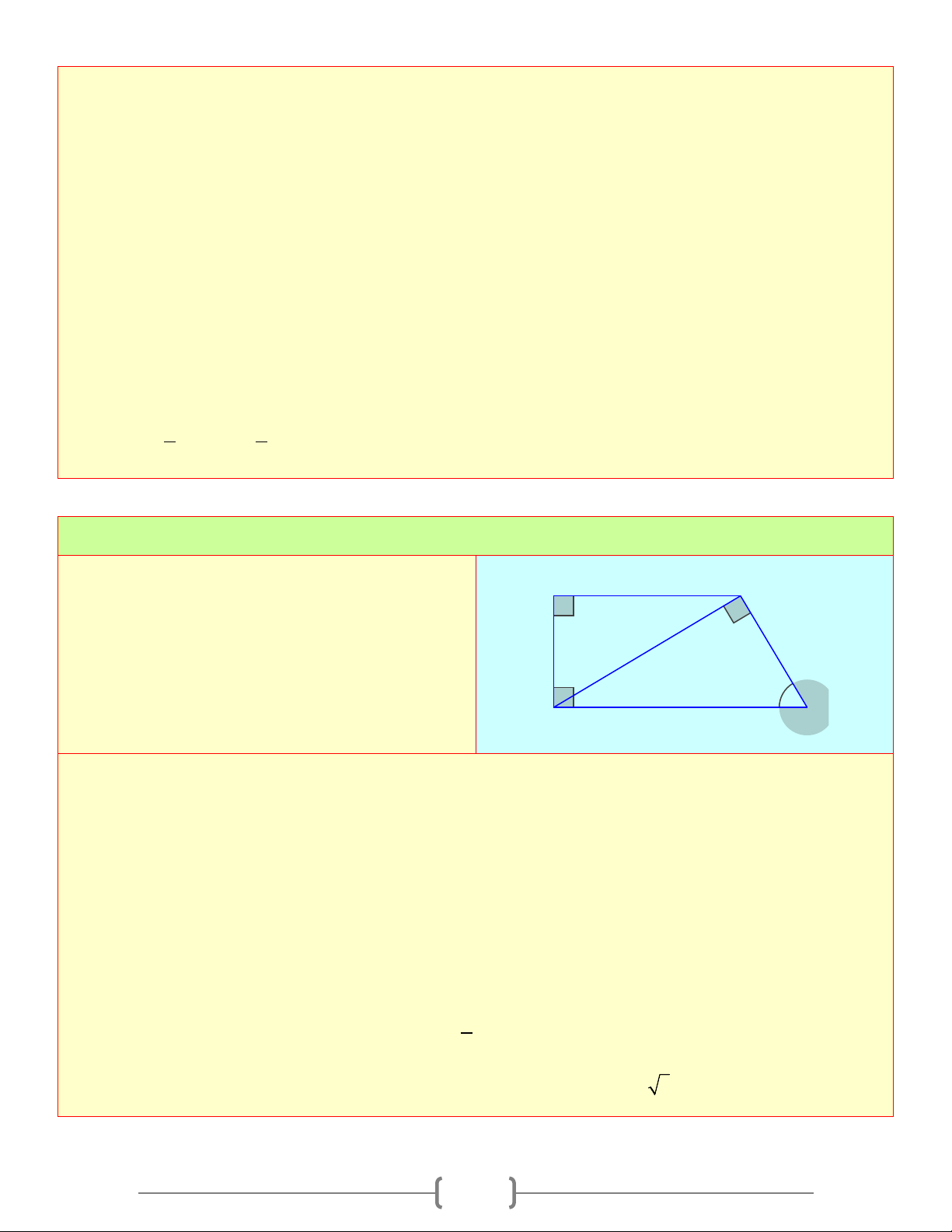
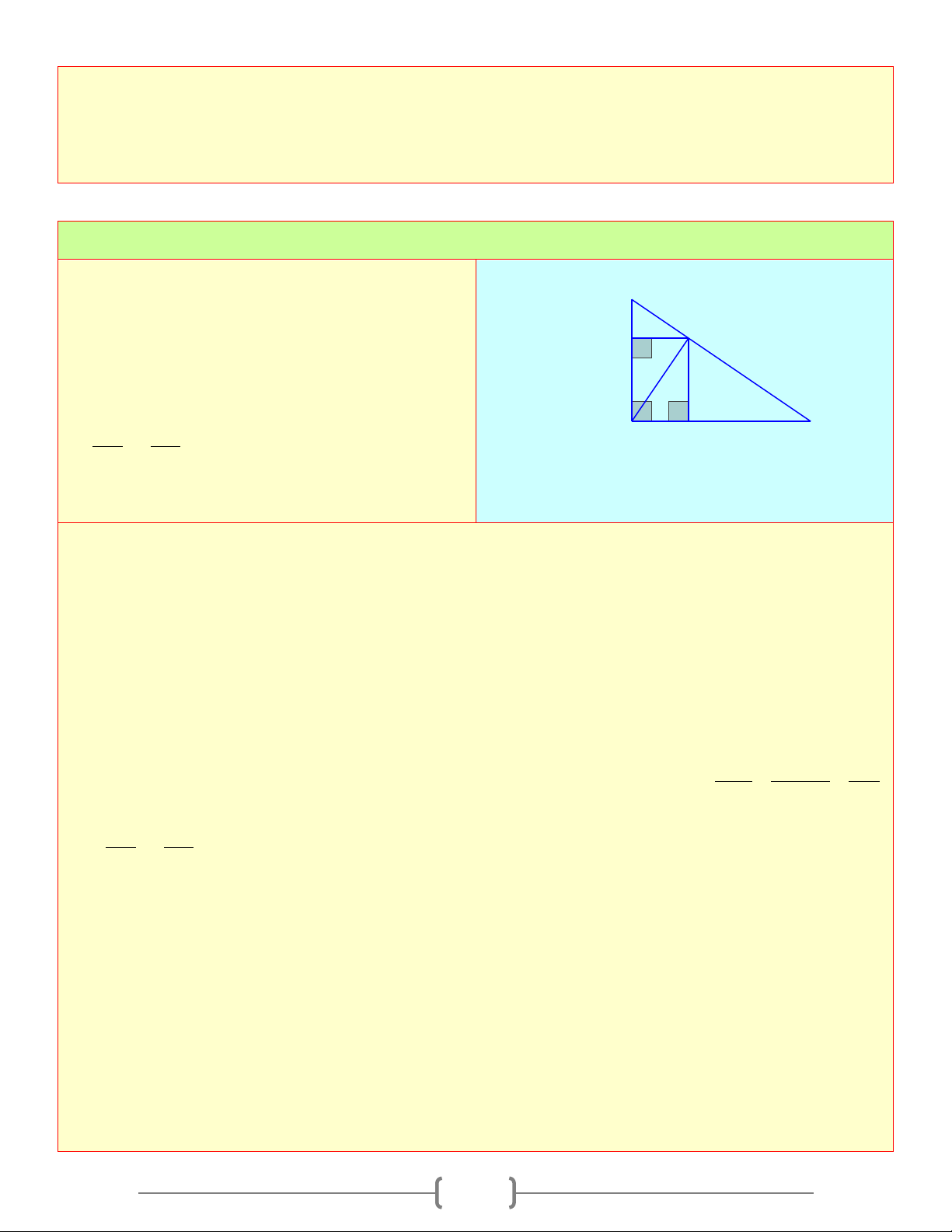
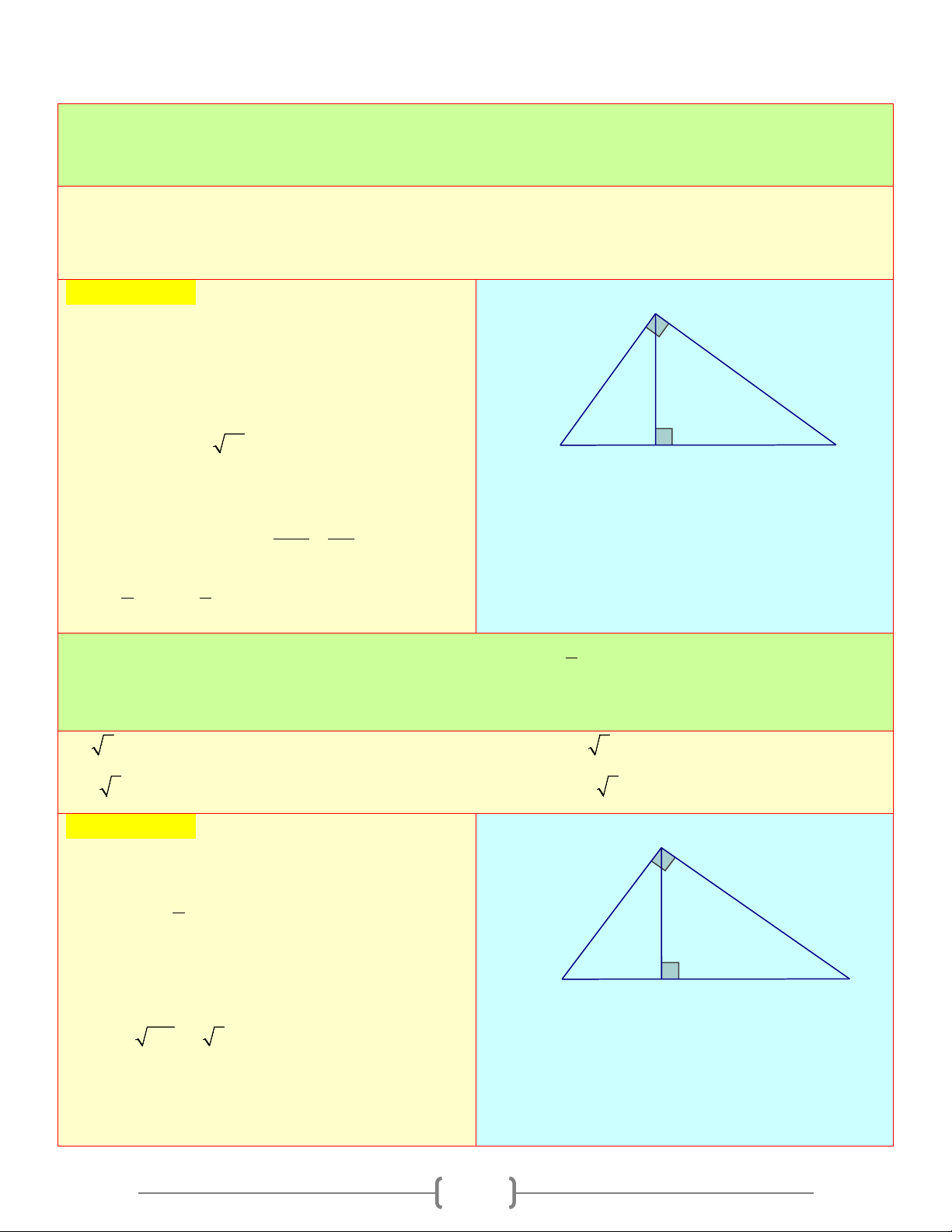
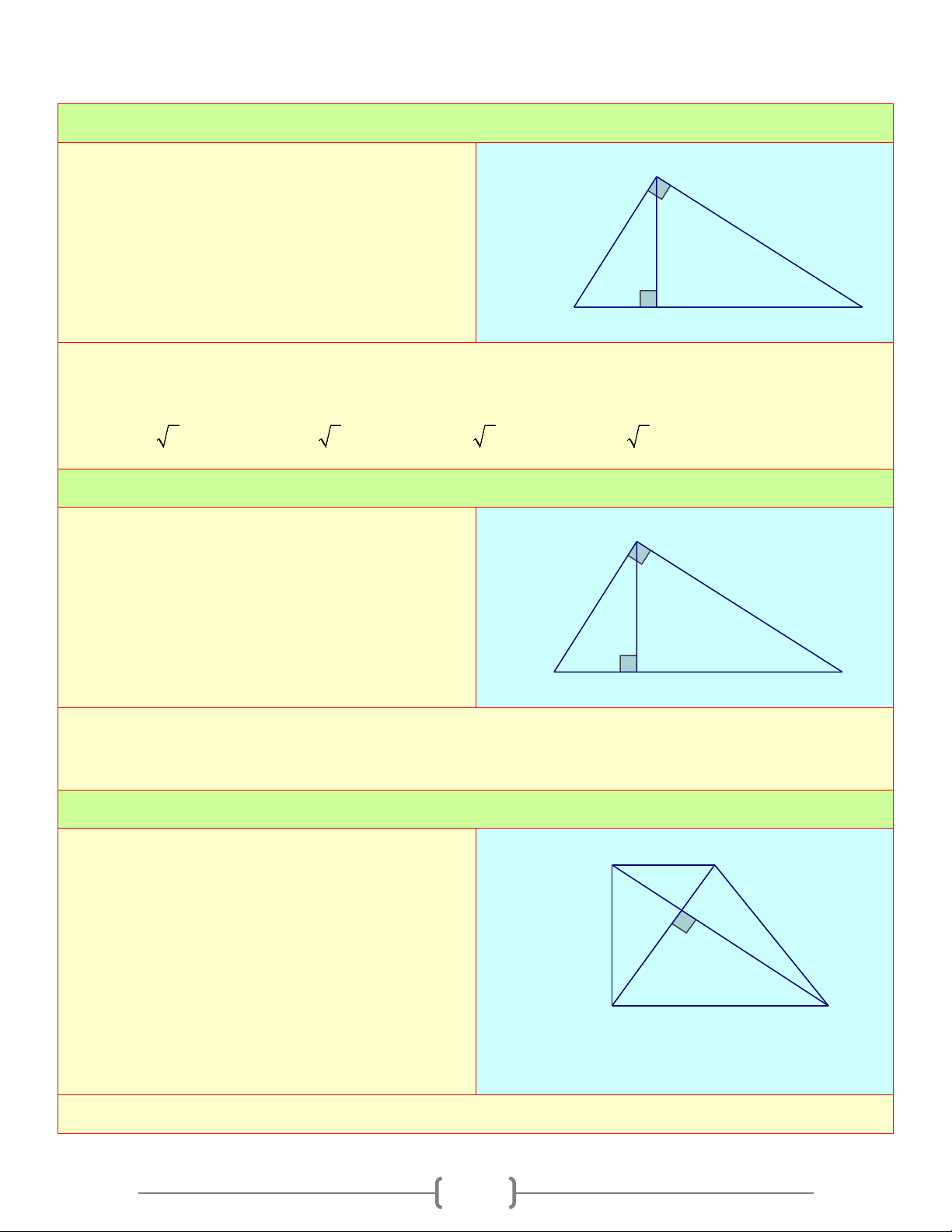
Tam giác ABC vuông tại A , đường cao AH , ta có: A
1) Hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền b c
Định lí 1: Trong một tam giác vuông, bình phương h
mỗi cạnh góc vuông bằng tích của cạnh huyền và H b' c' B C
hình chiếu của cạnh góc vuông đó trên cạnh huyền a Ta có: 2
AB = BH.BC ; 2
AC = HC.BC
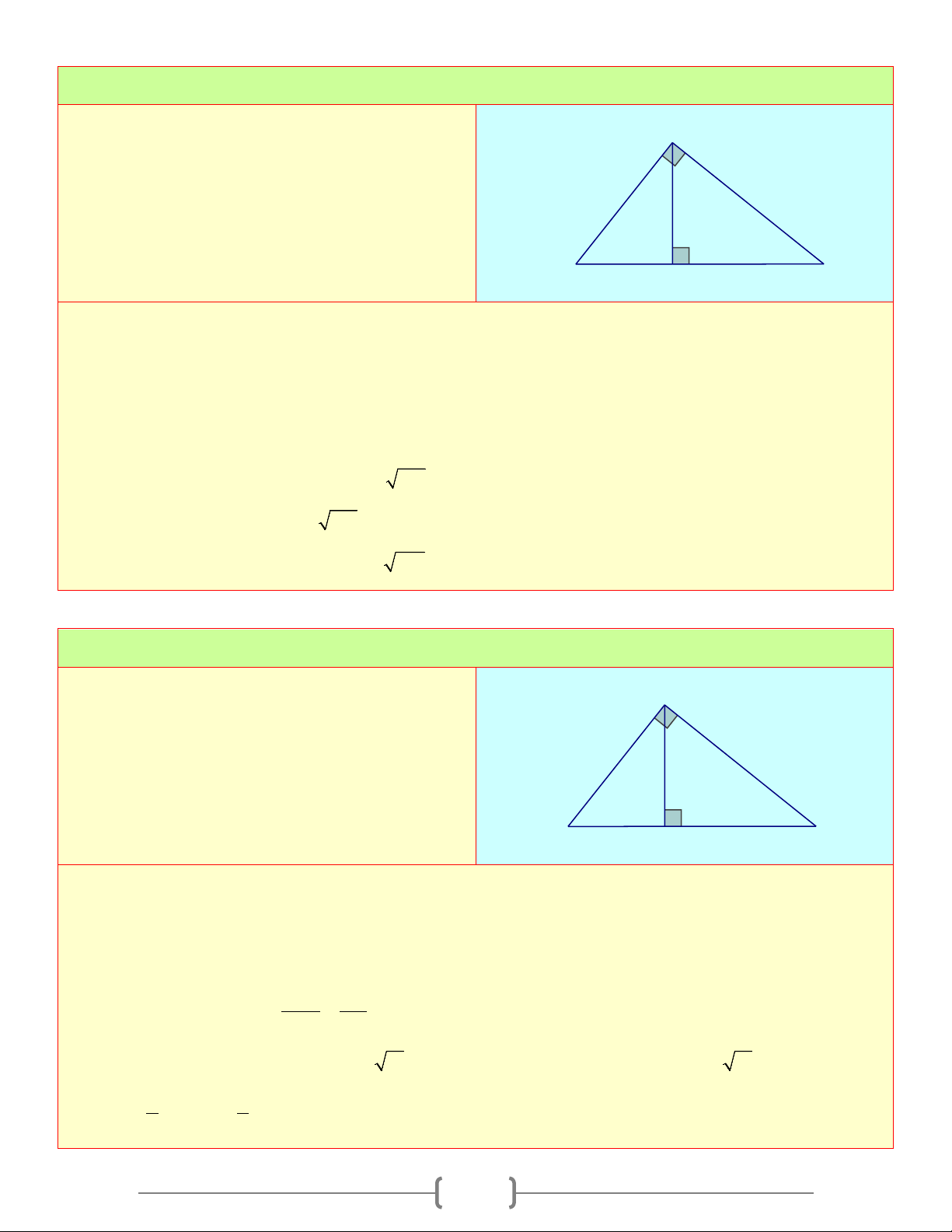
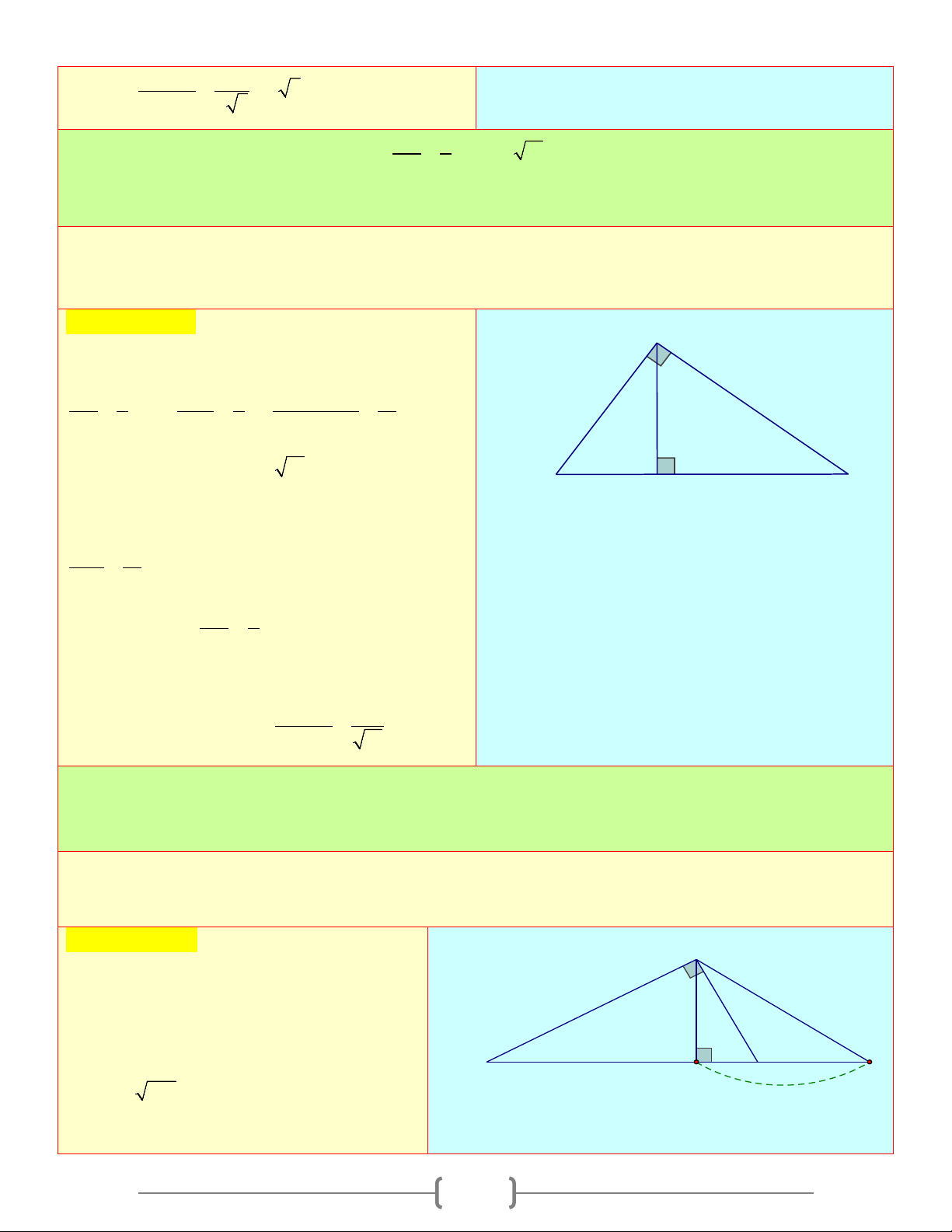
2) Hệ thức liên qua tới đường cao
Định lí 2: Trong một tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng tích
hai hình chiếu của hai cạnh góc vuông trên cạnh huyền Ta có: 2
AH = BH.HC
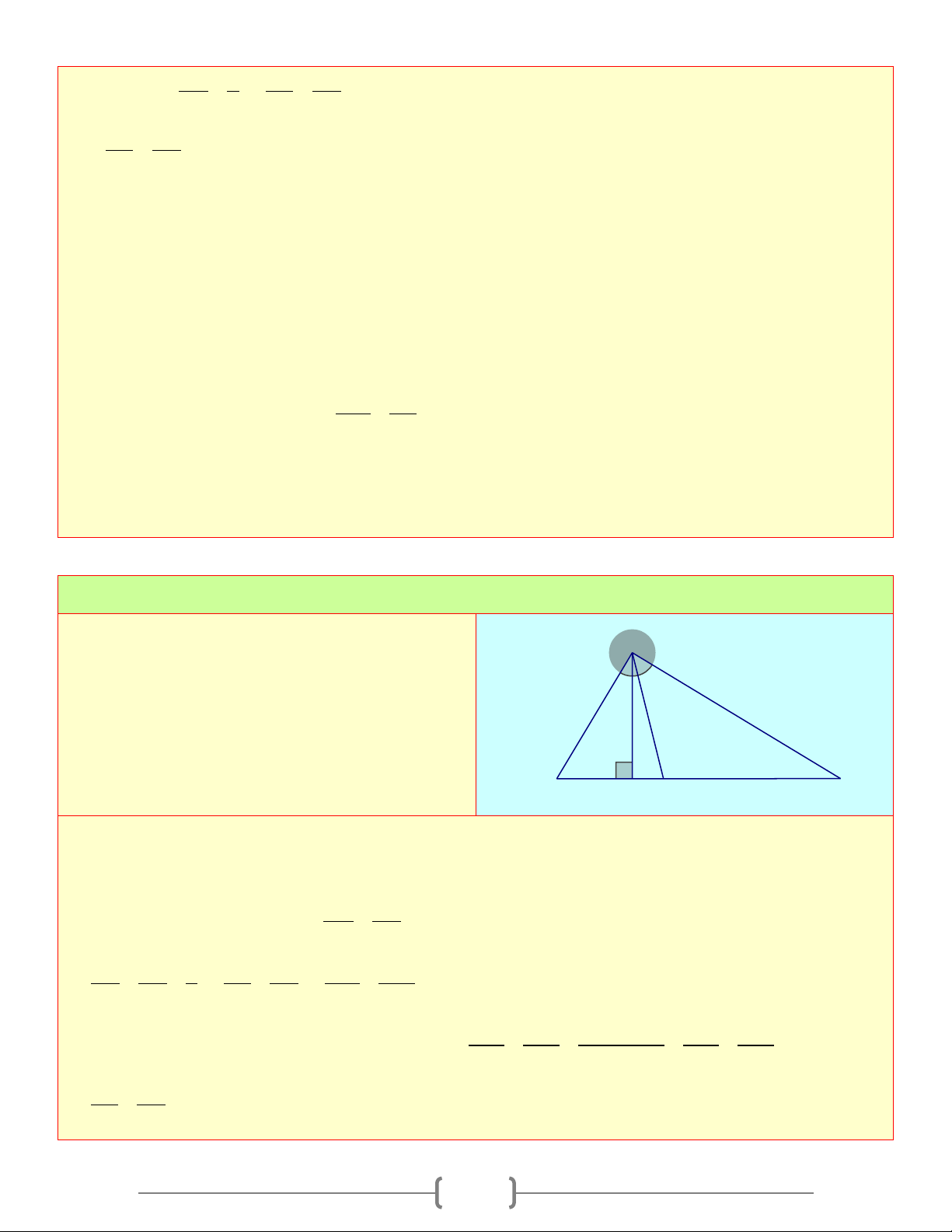
Định lí 3: Trong một tam giác vuông, tích hai cạnh góc vuông bằng tích của cạnh huyền và đường cao tương ứng Ta có: A .
B AC = AH.BC
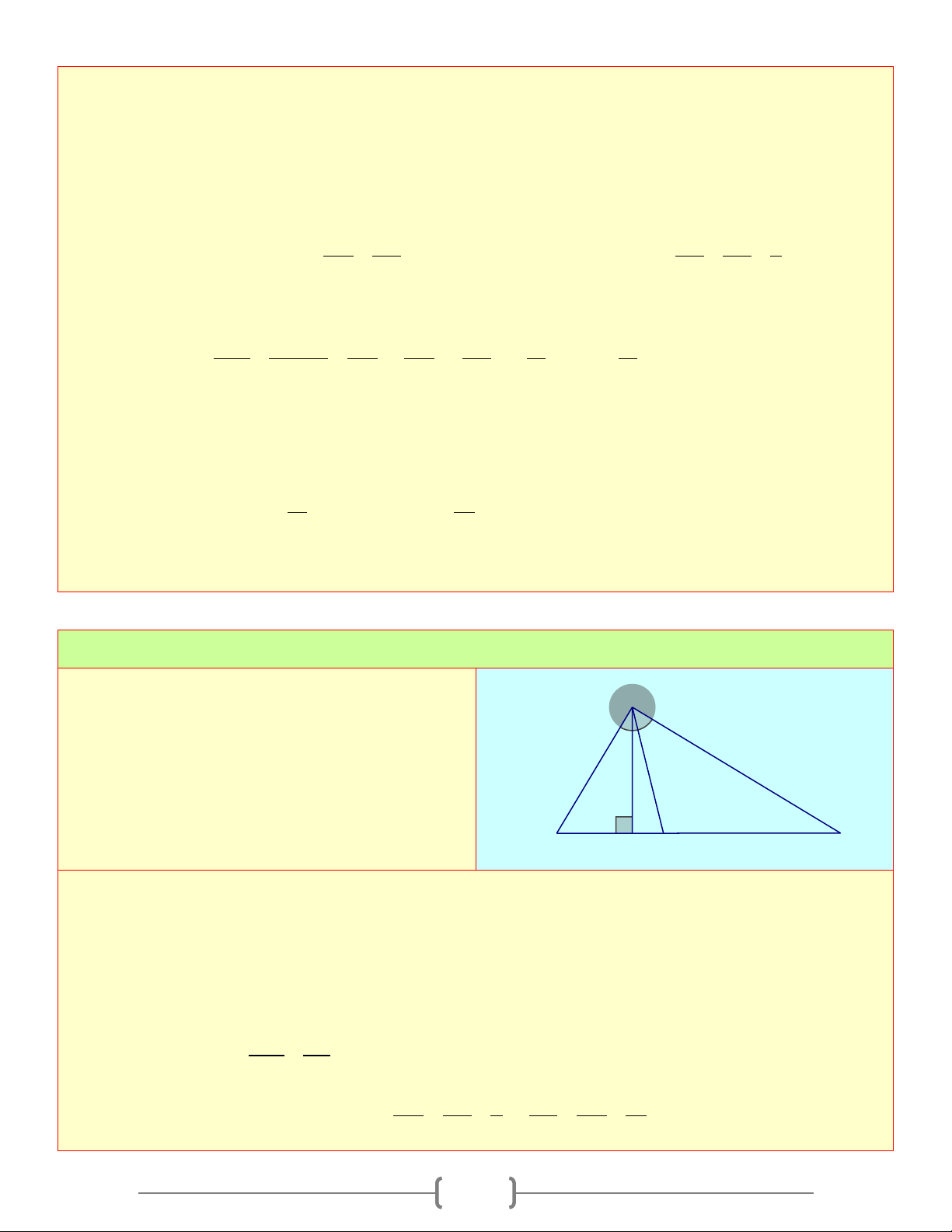
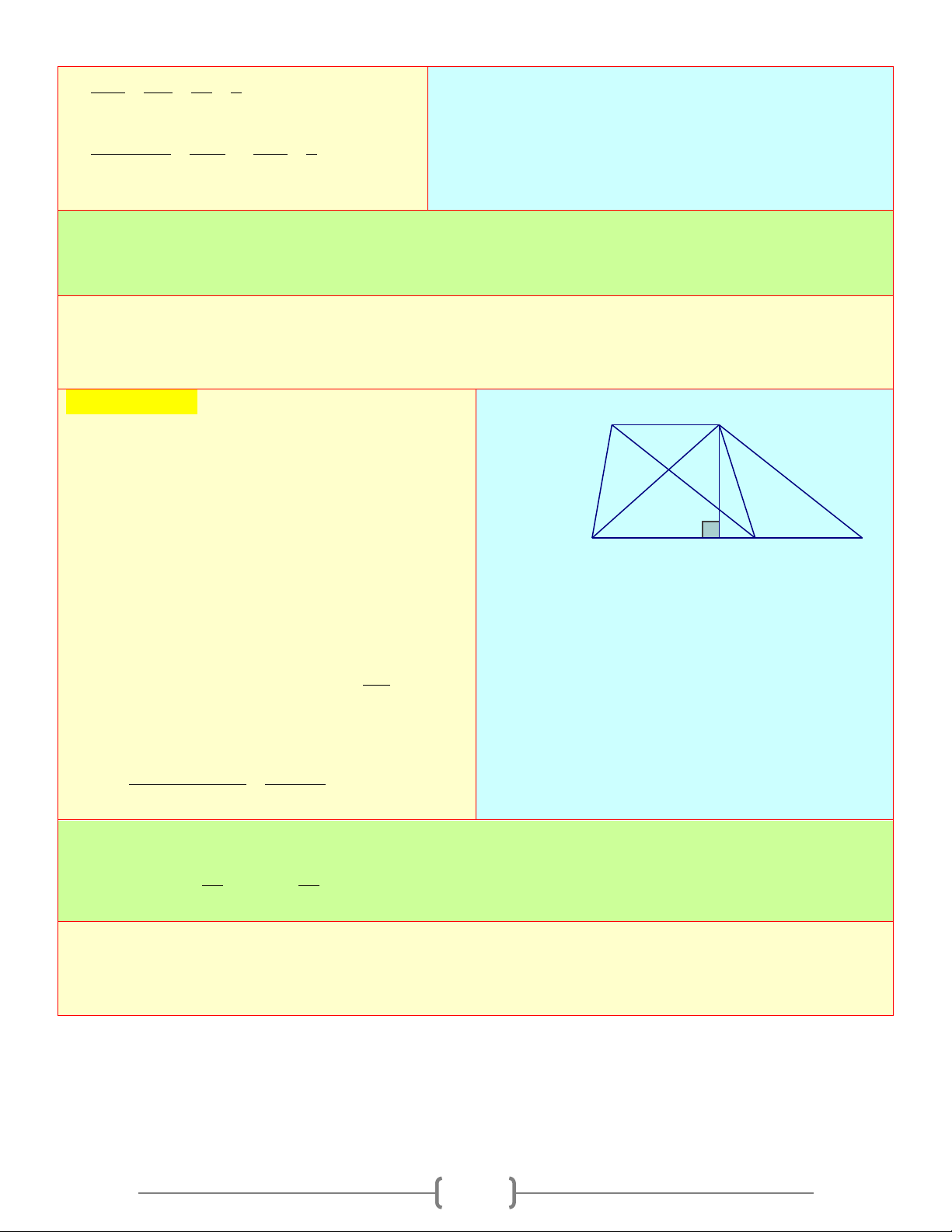
Định lí 4: Trong một tam giác vuông, nghịch đảo của bình phương đường cao ứng với cạn
huyền bằng tổng các nghịch đảo của bình phương hai cạnh góc vuông Ta có: 1 1 1 = + 2 2 2 AH AB AC
*) Tóm tắt các công thức 1) 2 2 2
a b c . 2) 2 2
b a.b ';c a.c ' 3) 2
h b '.c '
4) a.h  .bc . 5) 1 1 1   . 2 2 2 h b c 1
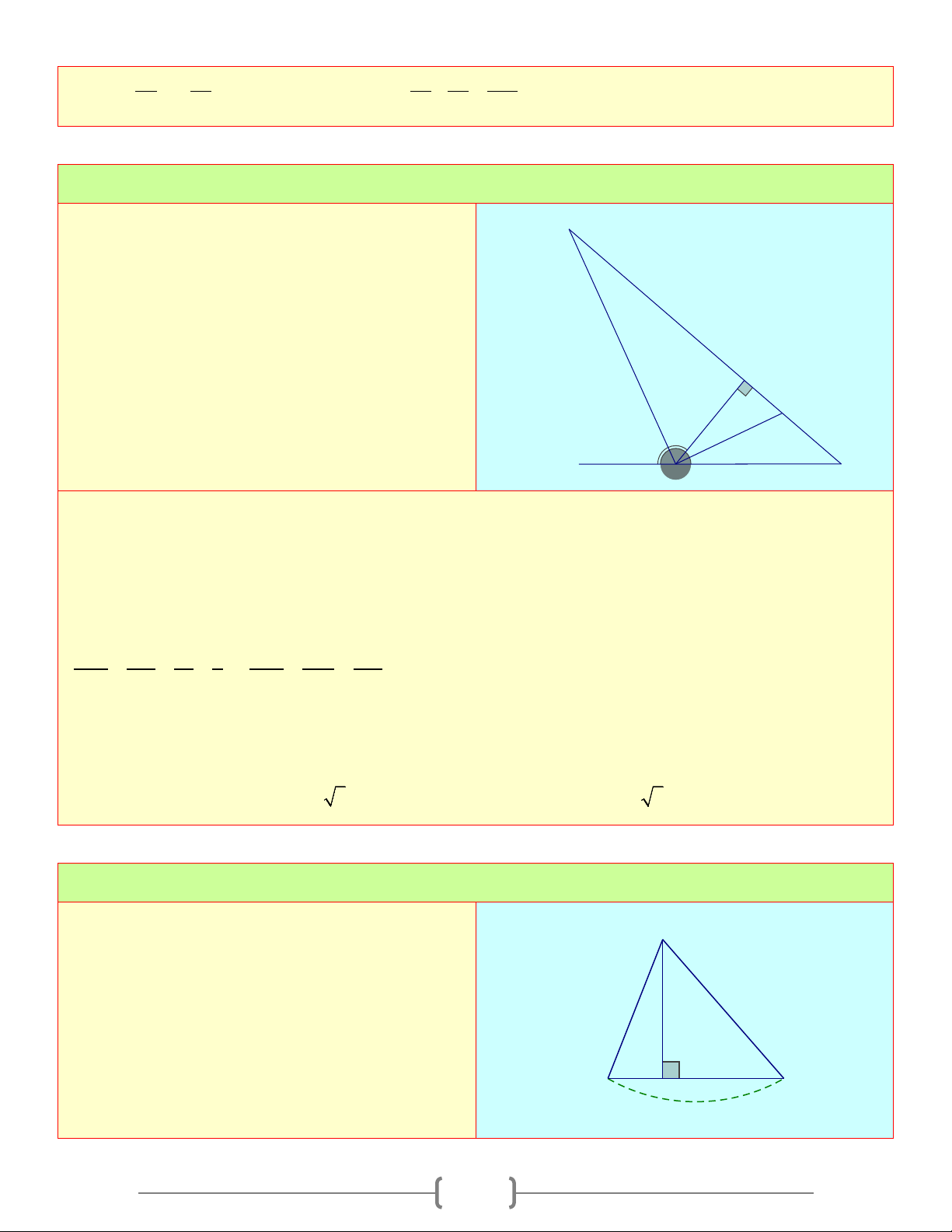
Chú ý: Diện tích tam giác vuông: 1 S ab 2
B. Bài tập và các dạng toán
Dạng 1: Tính độ dài các đoạn thẳng trong tam giác vuông Cách giải:
Bước 1: Xác định vai trò của đoạn thẳng đã biết và đoạn thẳng cần tính trong tam giác
vuông. Cụ thể, xác định xem đoạn thẳng đó là +) Là cạnh góc vuông +) Là đường cao +) Là cạnh huyền +) Là hình chiếu
Bước 2: Từ đó lựa chọn công thức tính phù hợp (trong 6 công thức ở phần lý thuyết) Xác định vai trò Lựa chọn công của các đoạn thức tính phù hợp thẳng
*) Lưu ý: Đôi khi phải dùng kĩ thuật đại số hóa để giải Chẳng hạn: - Nếu có AB m = thì đặt AB AC = = k ( ,
m n,k > 0) ⇒ AB = km và AC = kn AC n m n
- Nếu có BH = x ⇒ CH = BC − BH = BC − x
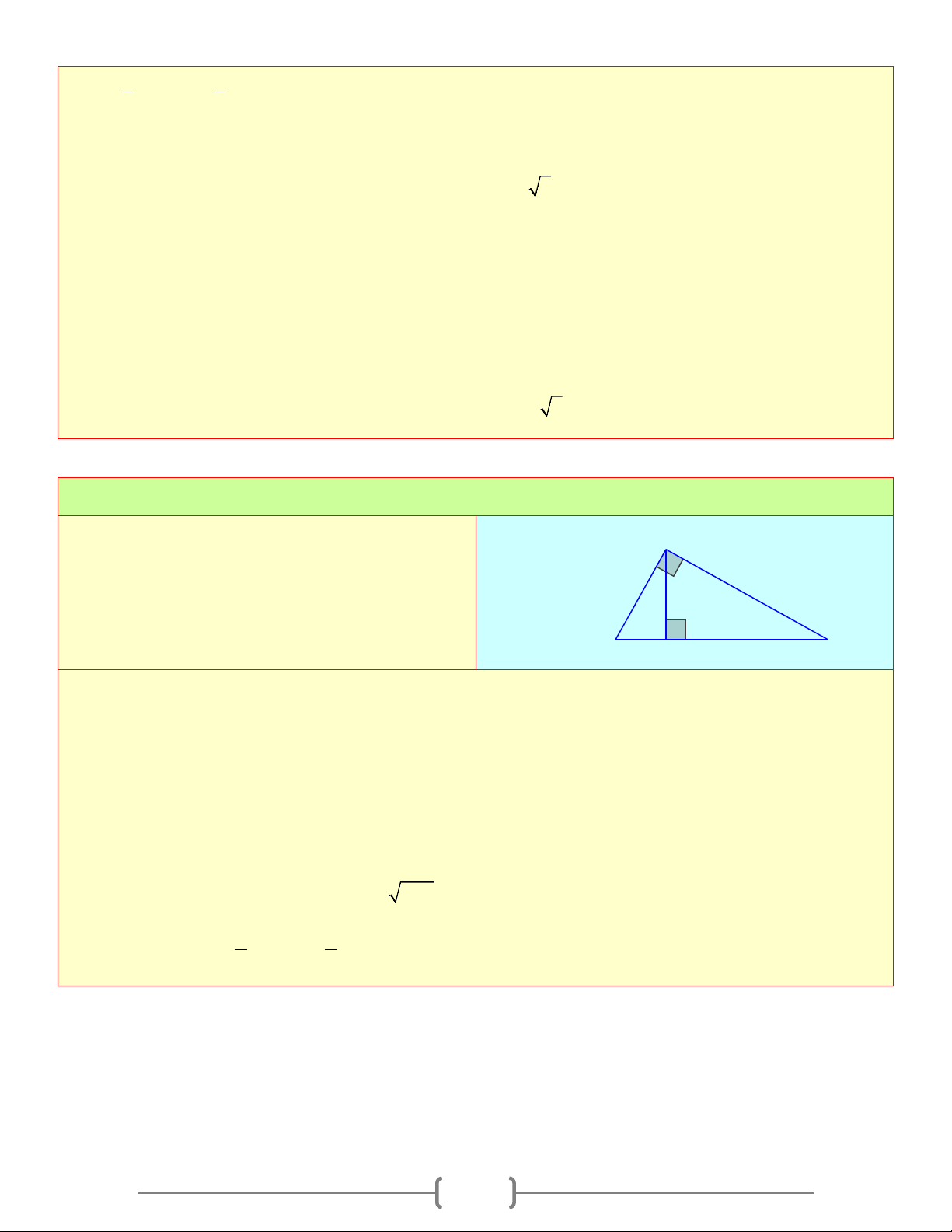
Bài 1: Tính x, y trong mỗi hình vẽ sau A A 8 6 x 7 5 B x y H C B H y C Lời giải a) Xét A ∆ BC vuông tại ,
A đường cao AH (H ∈ BC) , ta có: 2
x = 3,6(cm)
Dùng định lý Pytago tính được BC =10(cm) ⇒  y = 6, 4  (cm) b) Xét A ∆ BC vuông tại ,
A đường cao AH (H ∈ BC) , ta có:  35 74
Dùng định lý Pytago tính được x = (cm)
BC = 74 (cm) ⇒  74 y = 74  (cm)
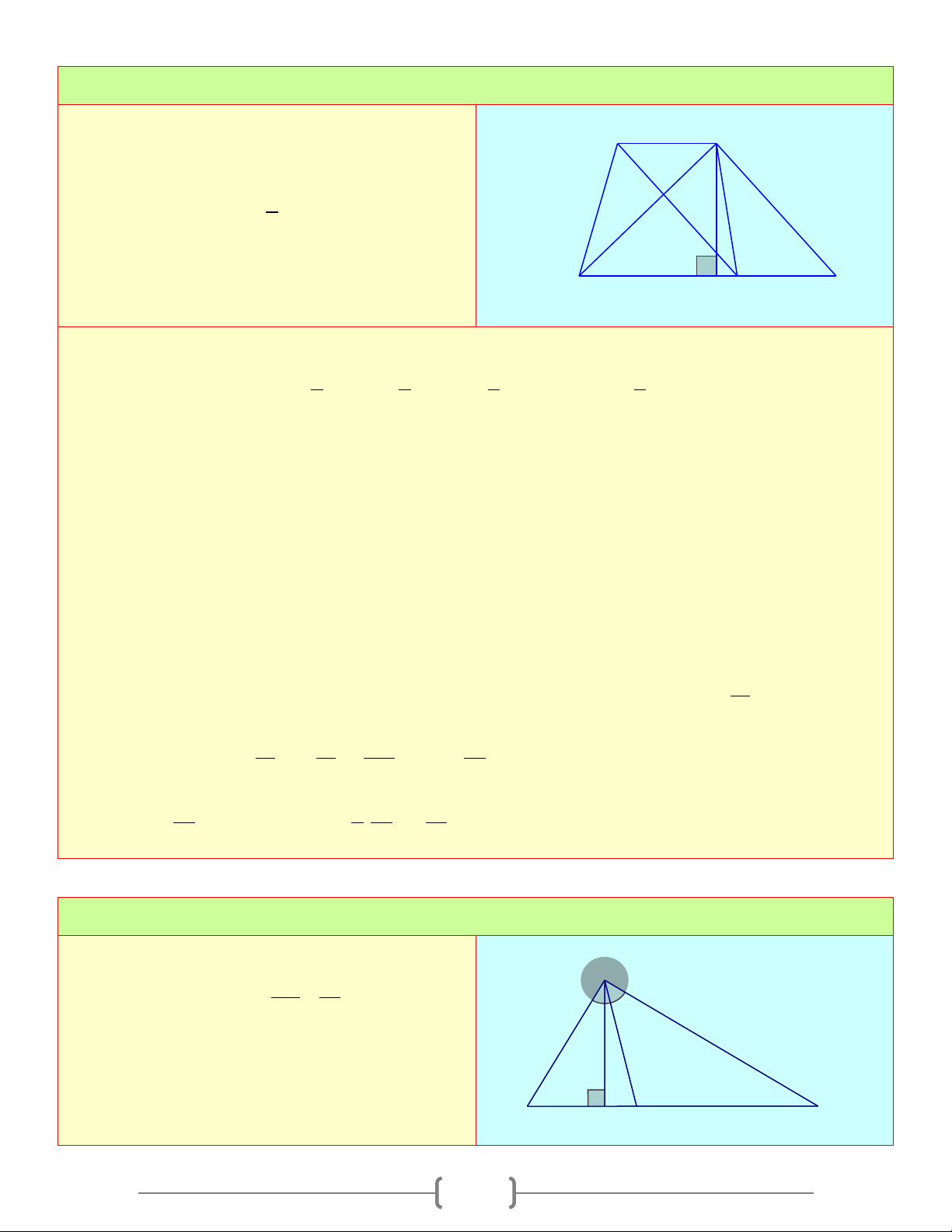
Bài 2: Tính x, y trong mỗi hình vẽ sau A A y x y 5 1 4 B H C B 7 x H C Lời giải a) Xét A ∆ BC vuông tại ,
A đường cao AH (H ∈ BC) , ta có: 2 2 AH = H .
B HC ⇔ AH = 4 ⇒ AH = 2 ⇒ x = 5 (cm); y = 2 5 (cm) b) Xét A ∆ BC vuông tại ,
A đường cao AH (H ∈ BC) , ta có: 2 2 AH 25 25
AH = HB HC ⇔ HC = = ⇒ x = (cm) 5 41 . ; y = (cm) HB 7 4 4
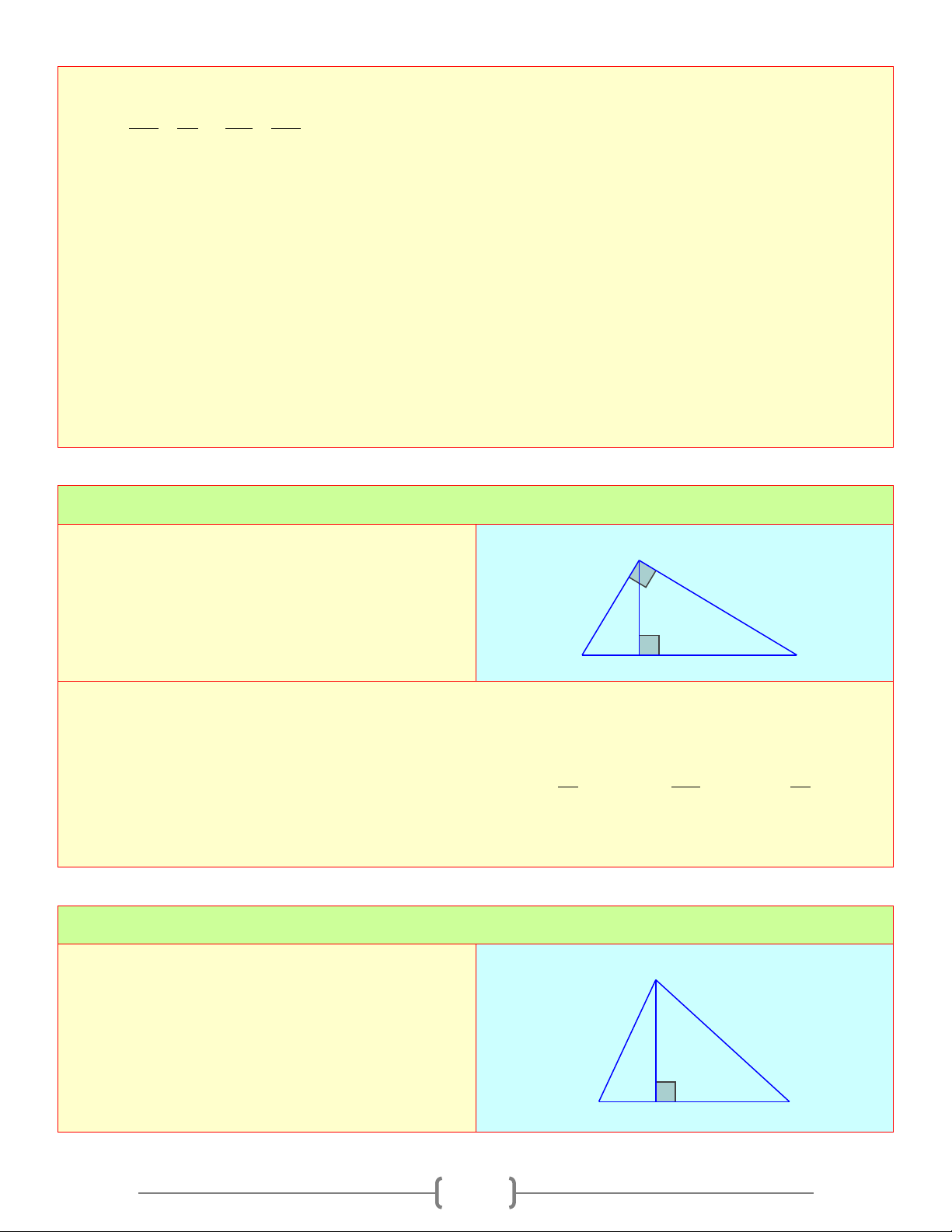
Bài 3: Tính x, y trong mỗi hình vẽ sau A A x 10 x 30 B y H 5 C B y H 32 C Lời giải 3 a) Xét A ∆ BC vuông tại ,
A đường cao AH (H ∈ BC) , ta có:
Áp dụng hệ thức về cạnh ta có: 2
b = b'.a , ta được: 2 = ( y + ) 9 10 8 8 ⇔ y = 2 2
Áp dụng hệ thức về cạnh: 2
c = c '.a , ta được: 2 9  9  15  15 x = 8 + = ⇔ x = (x >     0) 2  2   2  2
b) Áp dụng hệ thức về cạnh: 2
c = c '.a , ta được: 2
30 = y ( y + 32) ⇔ ( y −18)( y + 50) = 0 ⇔ y =18( y + 50 > 0)
Áp dụng hệ thức về cạnh: 2
b = b'.a , ta được: 2 x = ( + ) 2 2
32 32 18 ⇔ x = 40 ⇔ x = 40(x > 0) .
Bài 4: Tính x, y trong mỗi hình vẽ sau Cho A
∆ BC vuông tại A , đường cao A
AH (H ∈ BC)
a) Cho biết AB = 3(cm), BC = 5(cm) . Tính BH 4 3
CH, AC, AH
b) Cho biết BH = 9(cm),CH =16(cm). Tính độ B H 5 C
dài các đoạn thẳng AB, AC, BC, AH Lời giải a) Xét A ∆ BC vuông tại ,
A đường cao AH (H ∈ BC) , ta có: +) 2 9
AB = BH.BC ⇒ BH = =1,8(cm) ⇒ CH = 3,2(cm) 5 +) 2 2 AC = C .
B BC ⇒ AC = 5.3,2 =16 ⇒ AC = 4(cm) +) 1 1 1 1 1 1 1 = + = + = +
⇒ AH = 2,4(cm) 2 2 2 2 2 AH AB AC 3 4 9 16 b) Xét A ∆ BC vuông tại ,
A đường cao AH (H ∈ BC) , ta có: AB =15c , m AC = 20c , m BC = 25c , m AH =12cm 4 Bài 5:
Tính x, y trong mỗi hình vẽ sau, biết A AH = 5cm y y 5cm B x H x C Lời giải Xét A
∆ BC vuông tại A , đường cao AH
Áp dụng hệ thức về cạnh và đường cao ta có: + 2 2
AH = BH.CH ⇒ 5 = .xx ⇒ x = 5(cm) + 1 1 1 1 1 1 1 2 2 = + ⇒ = + ⇒ =
⇒ y = 50 ⇒ y = 5 2 cm . 2 2 2 2 2 2 2 ( ) AH AB AC 5 y y 25 y Bài 6: Cho A
∆ BC vuông tại A , đường cao A
AH (H ∈ BC) , có AC =10c ,
m AB = 8cm . Tính
BC, BH,CH, AH 10 8 B H C Lời giải a) Xét A ∆ BC vuông tại ,
A đường cao AH (H ∈ BC) , ta có: 2 2 2
BC = AB + AC ( pytago) ⇒ BC = 2 41(cm) 2 + 2 AB 64 32
AB = BH.BC ⇒ BH = = = (cm) BC 2 41 41 + 32 50
CH = BC − BH = 2 41 − = (cm) 41 41 + 1 1 1 1 1 1 1 = + = + = +
⇒ AH = 6,4(cm) 2 2 2 2 2 AH AB AC 8 10 64 100 5 Bài 7: Cho A
∆ BC vuông tại A , đường cao A
AH (H ∈ BC) , có BH =10c ,
m CH = 42cm . Tính
BC, AH, AB, AC B 10 H 42 C Lời giải a) Xét A ∆ BC vuông tại ,
A đường cao AH (H ∈ BC) , ta có:
- BC = BH + HC =10 + 42 = 52(cm)
Áp dụng hệ thức lượng trong tam giác vuông ta có: +) 2
AB = BH.BC =10.52 = 520 ⇒ AB = 2 130(cm) +) 2 2 2
AH = AB − BH ⇒ AH = 2 105(cm) +) 2 2 2
AC = AH + HC ( pytago) ⇒ AC = 2 546(cm) Bài 8: Cho A
∆ BC vuông tại A , đường cao A
AH (H ∈ BC) , có BH =10c ,
m CH = 42cm . Tính
BC, AH, AB, AC 12 B 9 H C Lời giải a) Xét A ∆ BC vuông tại ,
A đường cao AH (H ∈ BC) , ta có:
Áp dụng hệ thức lượng trong tam giác vuông ta có: 2 2 +) 2 AH 12
AH = BH.CH ⇒ CH = =
= 16 ⇒ CH = 4(cm) 2 BH 9 +) 2 2
AB = BH.BC = 9.13 =112 ⇒ AB = 3 13(cm); AC = BC.CH =13.4 = 52 ⇒ AC = 2 13(cm) +) 1 1 2 S = AH BC = = cm ABC . .12.13 78( ) 2 2 6 +) Chu vi A
∆ BC = AB + BC + CA = 3 13 + 2 13 +13 =13+ 5 13(cm) Bài 9:
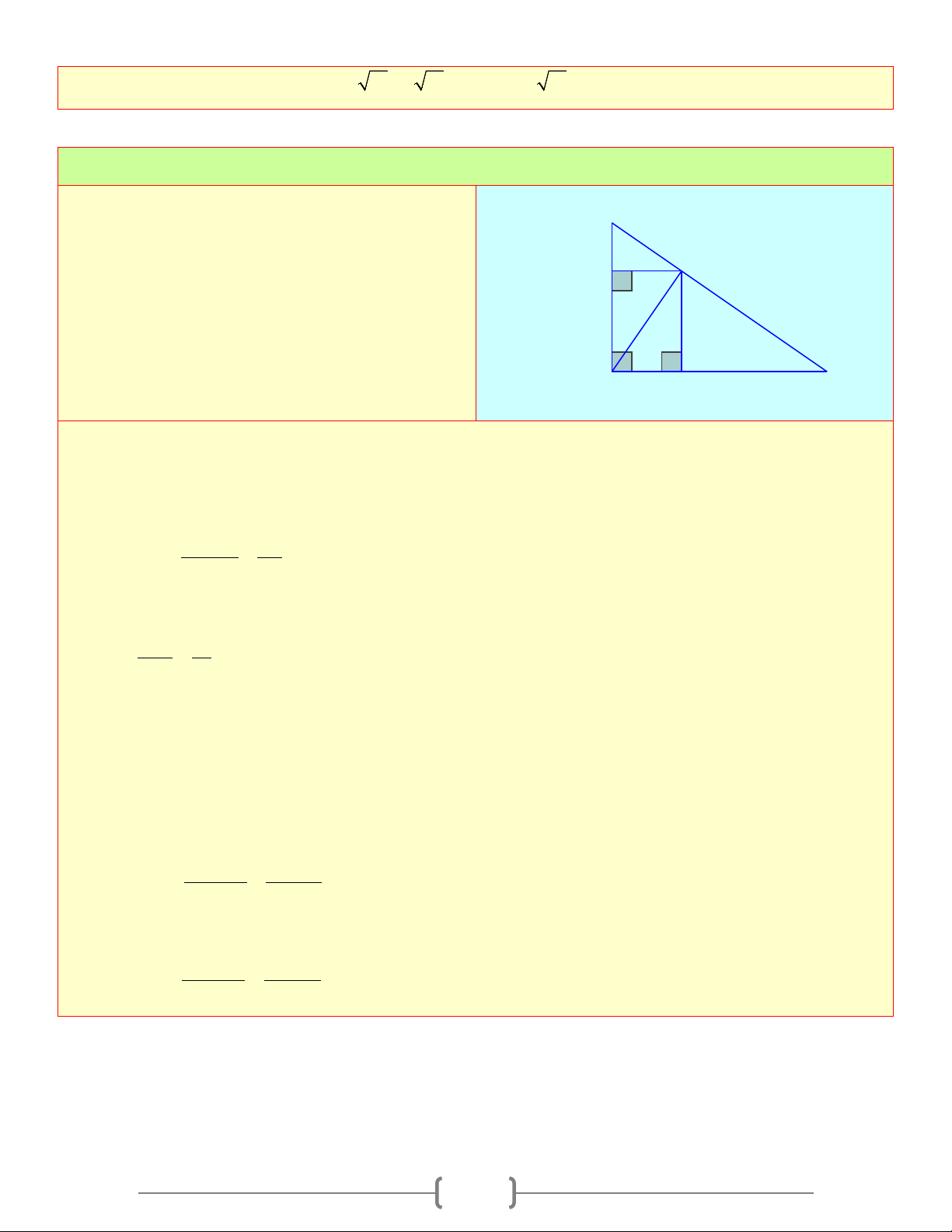
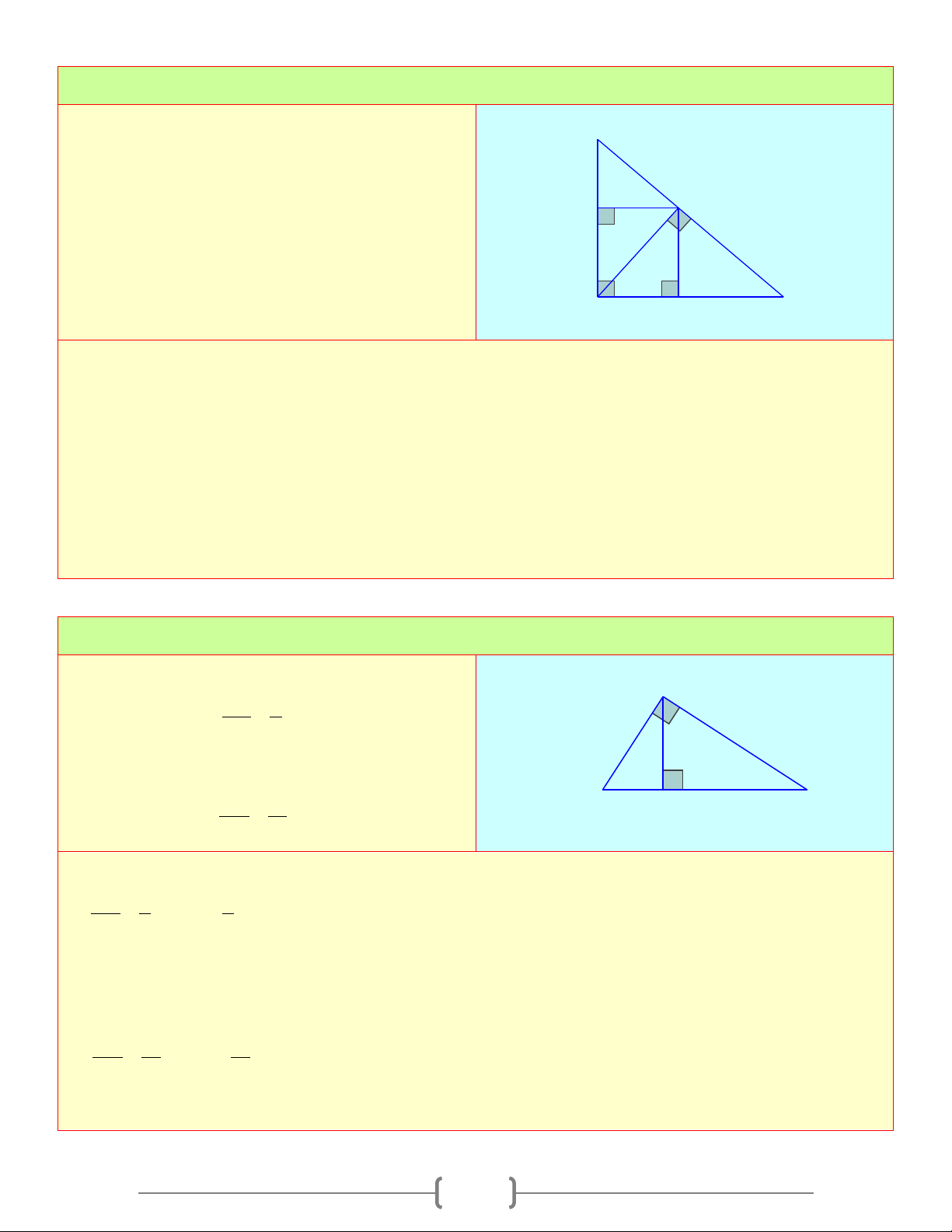
Cho tam giác ABC có AB = 6c , m AC = 8cm và B BC =10cm H
a) Chứng minh tam giác ABC vuông M
b) Tính đường cao AH
c) Gọi M, N lần lượt là hình chiếu của H trên AB A
, AC . Tính HM , HN N C Lời giải a) A ∆ BC có 2 2 2
BC = AB + AC (vì 2 2 2 10 = 6 + 8 )⇒ A
∆ BC vuông tại A (định lí pitago đảo) b) Xét A
∆ BC vuông tại A , đường cao AH có: A .
B AC = AH.BC (hệ thức về cạnh và đường cao) A . B AC 6.8 ⇒ AH = = = 4,8(cm) BC 10 c) Xét A
∆ BC vuông tại A , đường cao AH có: 2
AH = BH.BC (hệ thức về cạnh và đường cao) 2 2 AB 6 ⇒ BH = = = 3,6(cm) BC 10
⇒ CH = BC = BH =10 − 3,6 = 6,4(cm)
+ Vì M, N lần lượt là hình chiếu của H trên AB, AC ⇒ HM ⊥ AB, HN ⊥ AC
+ AH ⊥ BC ⇒  = 
AHB AHC . Do đó các tam giác A ∆ BH, A
∆ CH vuông tại H + Xét A
∆ BH vuông tại H , đường cao HM , có MH.AB = BH.AH (hệ thức về cạnh và đường cao) BH.AH 3,6.4,8 ⇒ MH = = = 2,88(cm) AB 6 + Xét A
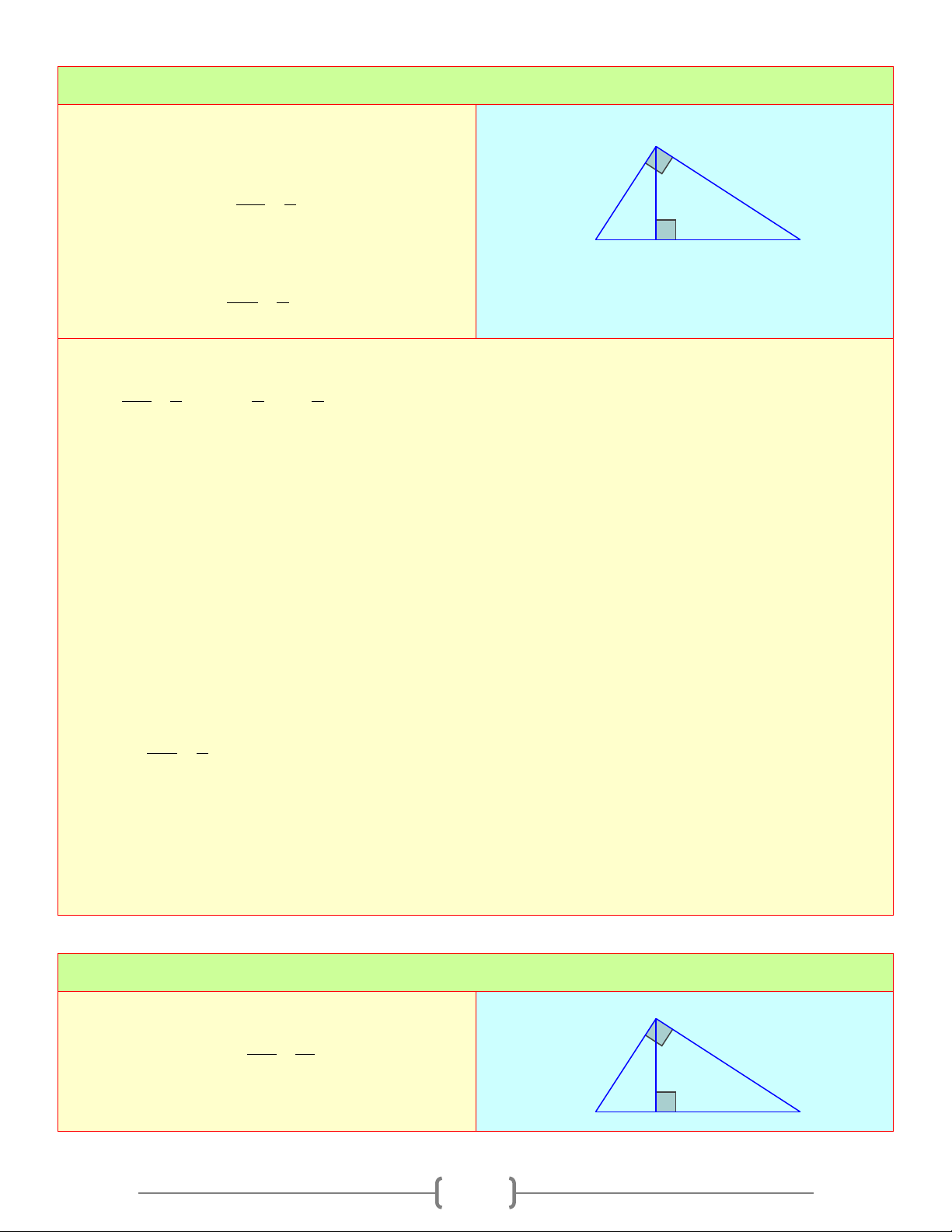
∆ CH vuông tại H , đường cao HN , có HN.AC = AH.CH (hệ thức về cạnh và đường cao) CH.AH 6,4.4,8 ⇒ NH = = = 3,84(cm) . AC 8 7 Bài 10:
Cho tam giác ABC vuông tại A , đường cao A AH a) Biết AB 3 AC =16c , m
= . Tính AB, BC, AH AC 4 BH,CH B H C b) Biết HB 1 AH =14c , m = . Tính BC HC 4 Lời giải a) Có AB 3 3 3
= ⇒ AB = AC = .16 =12(cm) AC 4 4 4 Xét A
∆ BC vuông tại A , đường cao AH có 2 2 2
BC = AB + BC (định lí pitago) 2 2 2
⇒ BC =12 +16 = 400 ⇒ BC = 20(cm) Hơn nữa lại có 2
AB = BH.BC (hệ thức giữa cạnh và đường cao) 2 2
⇒ BH = AB : BC =12 : 20 = 7,2(cm)
HC = BC − BH = 20 − 7,2 =12,8(cm) Mặt khác 2
AH = BH.HC = 7,2.12,8 = 92,16 ⇒ AH = 9,6(cm) Vậy AB =12c , m BC = 20c , m AH = 9,6c , m BH = 7,2c , m HC =12,8cm b) Ta có HB 1
= ⇒ CH = 4BH ( ) 1 HC 4 Xét A
∆ BC vuông tại A , đường cao AH , có 2 AH = . HB HC (2) Từ (1)(2) suy ra 2 2 2 2 AH = 4 .
HB HB ⇔ 14 = 4HB ⇒ BH = 49 ⇒ BH = 7(cm) ⇒ CH = 4.7 = 28(cm)
Vậy BC = BH + HC = 7 + 28 = 35(cm). Bài 11:
Cho tam giác ABC vuông tại A , đường cao A AH . Biết AB 5 BC = 26c , m = . Tính AB, AC AC 12
Và AH, BH,CH B H 26 C 8 Lời giải 2 2
Cách 1: Từ giả thiết AB 5 AB AC AB AC = ⇒ = ⇒ = AC 12 5 12 25 144 2 2 2 2 2 2
Áp dụng tính chất dãy tỉ số bằng nhau ta có AB AC AB + AC BC 26 = = = = = 4 25 144 25 +144 169 169 AB AC ⇒ =
= 2 ⇒ AB =10(cm), AC = 24(cm) 5 12 Xét A
∆ BC vuông tại A , đường cao AH , có 2 2 2 50
AB = BH.BC ⇒ BH = AB : BC =10 : 26 = (cm) 13 50 288
⇒ HC = BC − BH = 26 − = (cm) 13 13 Mặt khác 2 50 288 14400 120
AH = BH.CH = . = ⇒ AH = (cm) 2 13 13 13 13 Vậy 120 50 288 AB =10c , m AC = 24c , m AH = c , m BH = c , m HC = cm 13 13 13
Cách 2: Dùng phương pháp đại số Từ giả thiết AB 5 AB AC = ⇒ = AC 12 5 12 Đặt AB AC =
= k (k > 0) ⇒ AB = 5k, AC =12k 5 12 Xét A
∆ BC vuông tại A , có 2 2 2
BC = AB + AC (định lí pitago)
Hay 2 = ( k)2 + ( k)2 2 26 5 12
⇒ k = 4 ⇒ k = 2(k > 0) Suy ra AB =10c , m AC = 24cm . Bài 12: Cho A
∆ BC vuông tại A , đường cao AH . Biết A AB 3 AH =12c , m
= . Tính AB, AC, BC, BH,CH AC 4 B H C Lời giải 9 Từ giả thiết AB 3 AB AC = ⇒ = AC 4 3 4 Đặt AB AC =
= k (k > 0) ⇒ AB = 3k (cm); AC = 4k (cm) 3 4 Xét A
∆ BC vuông tại A , đường cao AH có 2 2 2 2
BC = AB + AC ⇒ BC = ( k )2 + ( k )2 2 3 4
= 25k ⇒ BC = 5k (cm)
+ AH.BC = A .
B AC (hẹ thức về cạnh và đường cao) 2 2
⇒ 12.5k = 3k.4k ⇒ 60k =12k ⇒12k − 60k = 0 ⇔ k = 5
Do đó AB = 3.5 =15(cm); AC = 4.5 = 20(cm);BC = 5.5 = 25(cm) 2 2 Mặt khác 2 AB 15
AB = BH.BC ⇒ BH = = = 9(cm) BC 25
+ CH = BC − BH = 25−9 =16(cm)
Vậy AB =15(cm), AC = 20(cm), BH = 9(cm),CH =16(cm) Bài 13: Cho A
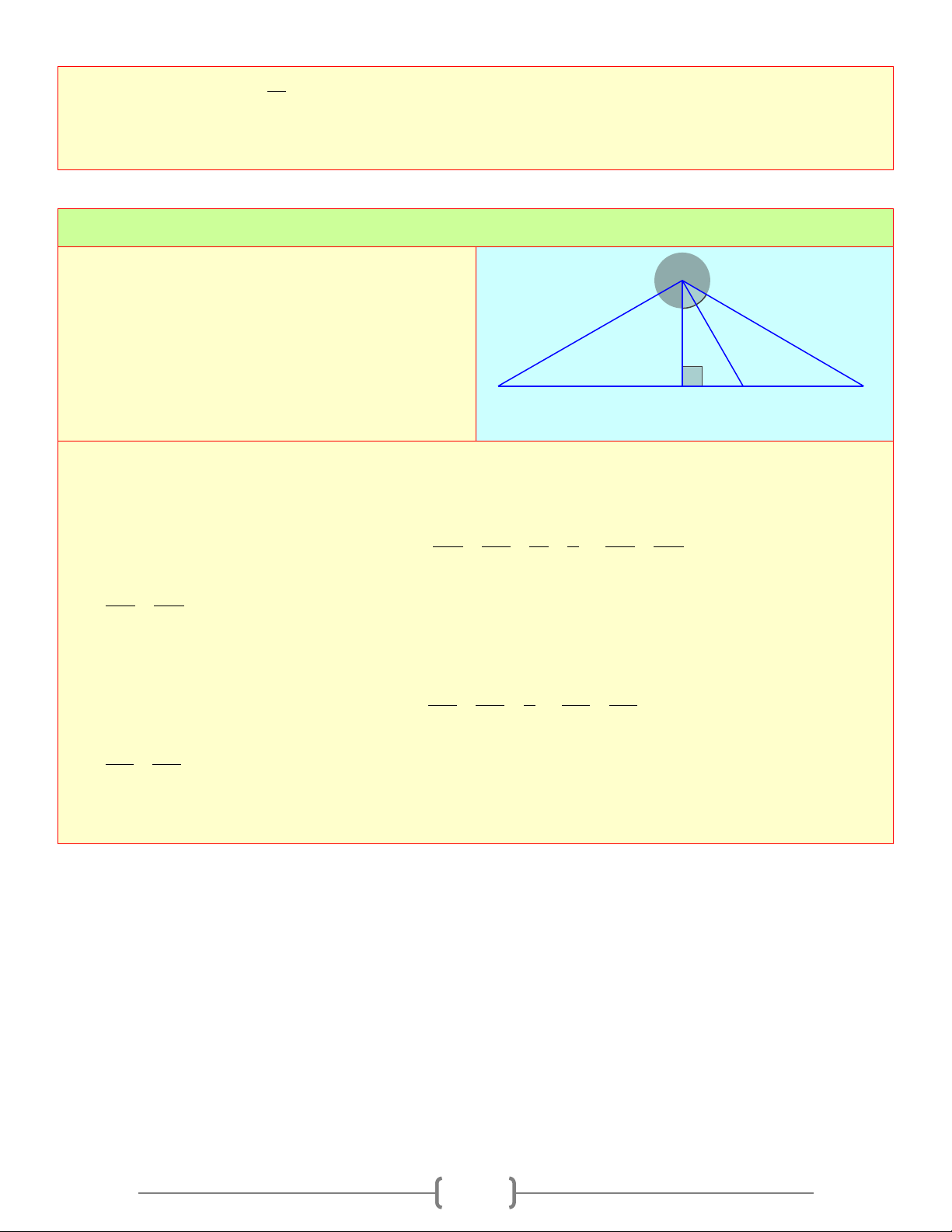
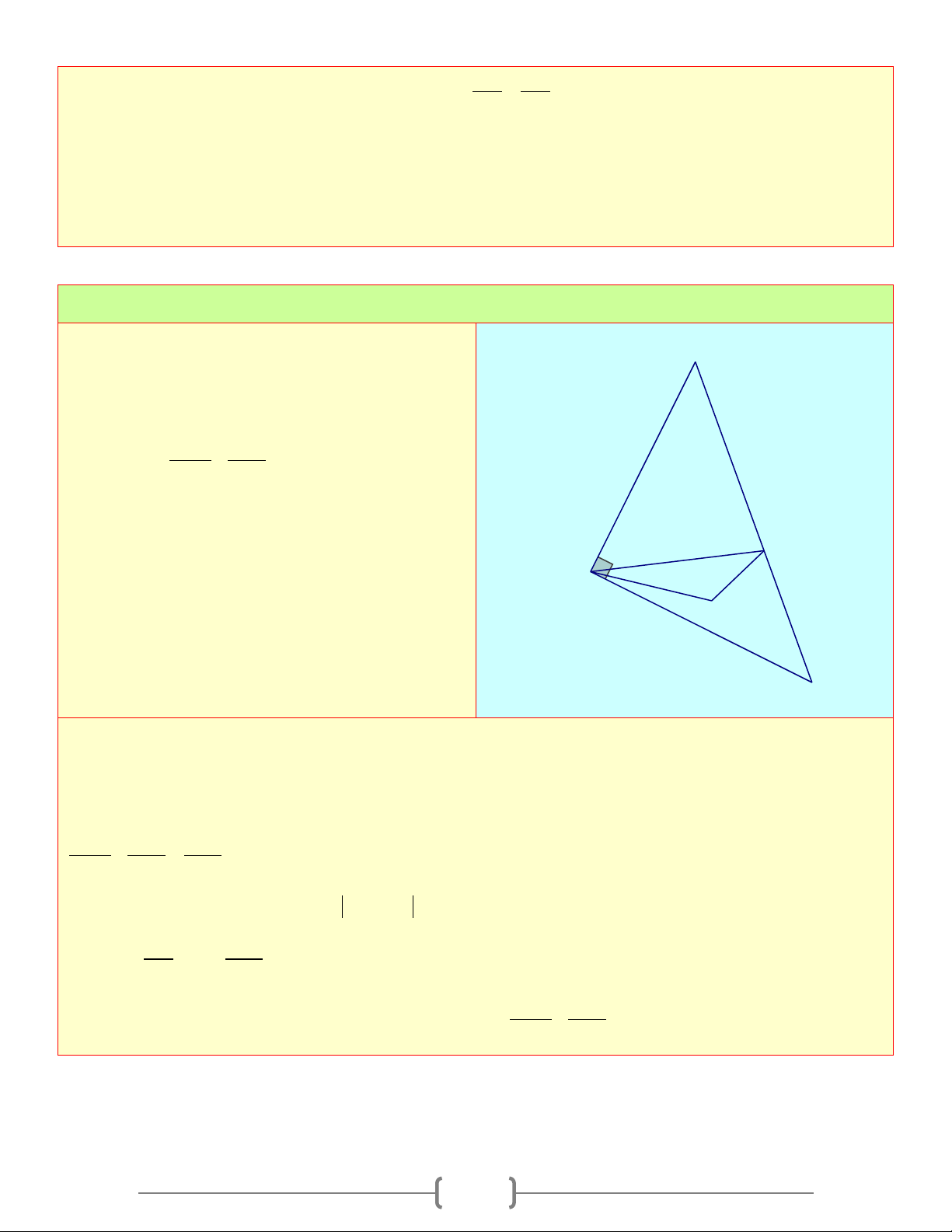
∆ BC vuông tại A , đường cao, phân A
giác trong AD . Biết BD = 75c , m DC =100cm . Tính BH,CH 16 12 B H D C Lời giải
Cách 1: Ta có BC = BD + DC = 75+100 =175(cm) A
∆ BC có AD là phân giác BD AB ⇒ =
(tính chất đường phân giác) DC AC 2 2 AB 75 3 AB AC AB AC ⇒ = = ⇒ = ⇒ = AC 100 4 3 4 9 16 2 2 2 2 2 2
Theo tính chất của dãy tỉ số bằng nhau, ta có: AB AC AB + AC BC 175 = = = = = 1225 9 16 25 25 25 AB AC ⇒ =
= 35 ⇒ AB = 3.35 =105(cm); AC = 4.35 =140(cm) 3 4 10 Xét A
∆ BC vuông tại A , đường cao AH có: 2 2 2
AB = BH.BC ⇒ BH = AB : BC =105 :175 = 63(cm)
CH = BC − BH =175 − 63 =112(cm) Vậy BH = 63c , m CH =112cm Cách 2: A
∆ BC có AD là phân giác BD AB ⇒ =
(tính chất đường phân giác) AB 75 3 ⇒ = = DC AC AC 100 4 Xét A
∆ BC vuông tại A , đường cao AH có: 2 2 2
AB = BH.BC  AB BH.BC BH BH AB  9 9  ⇒ = = ⇒ = = ⇒   BH = CH (1) 2 2
AC = CH.BCAC CH.BC CH CH   AC  16 16
Hơn nữa BC = BD + DC = 75+100 =175(cm)
Do đó BH +CBC =175(cm) (2)
Thay (1) vào (2) ta được 9 25 CH + CH =175 ⇔
CH =175 ⇔ CH =112(cm) 16 16
⇒ BH =175 −112 = 63(cm) . Bài 14: Cho A
∆ BC vuông tại A , đường cao A
AH (H ∈ BC) , biết AB =12c ;
m AC =16cm , Phân
giác trong AD . Tính độ dài đoạn HD 16 12 B H D C Lời giải Xét A ∆ BC vuông tại ,
A đường cao AH (H ∈ BC) , ta có: 2 2 2
AB + AC = BC ( pytago) ⇒ BC = 20(cm)
+) Áp dụng hệ thức lượng trong tam giác vuông ta có: 2 2 2 AB 12
AB = BC.BH ⇒ BH = = = 7,2(cm) BC 20
+) Ta có AD là phân giác của  BAC DB AB 3 BD DC 20 ⇒ = = ⇒ = = (cm) DC AC 4 3 4 7 11 20 60 60 36 552 ⇒ DB = .3 =
(cm) ⇒ HD = DB − BH = − = (cm) . 7 7 7 5 35 Bài 15: Cho A
∆ BC vuông tại A , có AB = 6cm , N BC =10c .
m Phân giác trong và ngoài tại đỉnh
B cắt AC lần lượt tại M và N . Tính BM , BN A M x B C Lời giải Xét A
∆ BC vuông tại A , đường cao AH ( H ∈ BC ), ta có: 2 2 2
AB + AC = BC ( pytago) ⇒ AC = 8(cm)
+) Áp dụng tính chất đường phân giác trong tam giác, ta có: AM AB 6 3 AM MC AC = = = ⇒ = =
= 1⇒ AM = 3(cm) MC BC 10 5 3 5 8
+) Áp dụng hệ thức lượng vào tam giác vuông BMN , ta có: 2
AB = AM.AN ⇒ 36 = 3.AN ⇒ AN =12(cm);MN = AM + AN =15(cm) 2 2
BM = MN.AM =15.3 ⇒ BM = 3 5(cm); BN = MN.AN =15.12 ⇒ BN = 6 5(cm) . Bài 16:
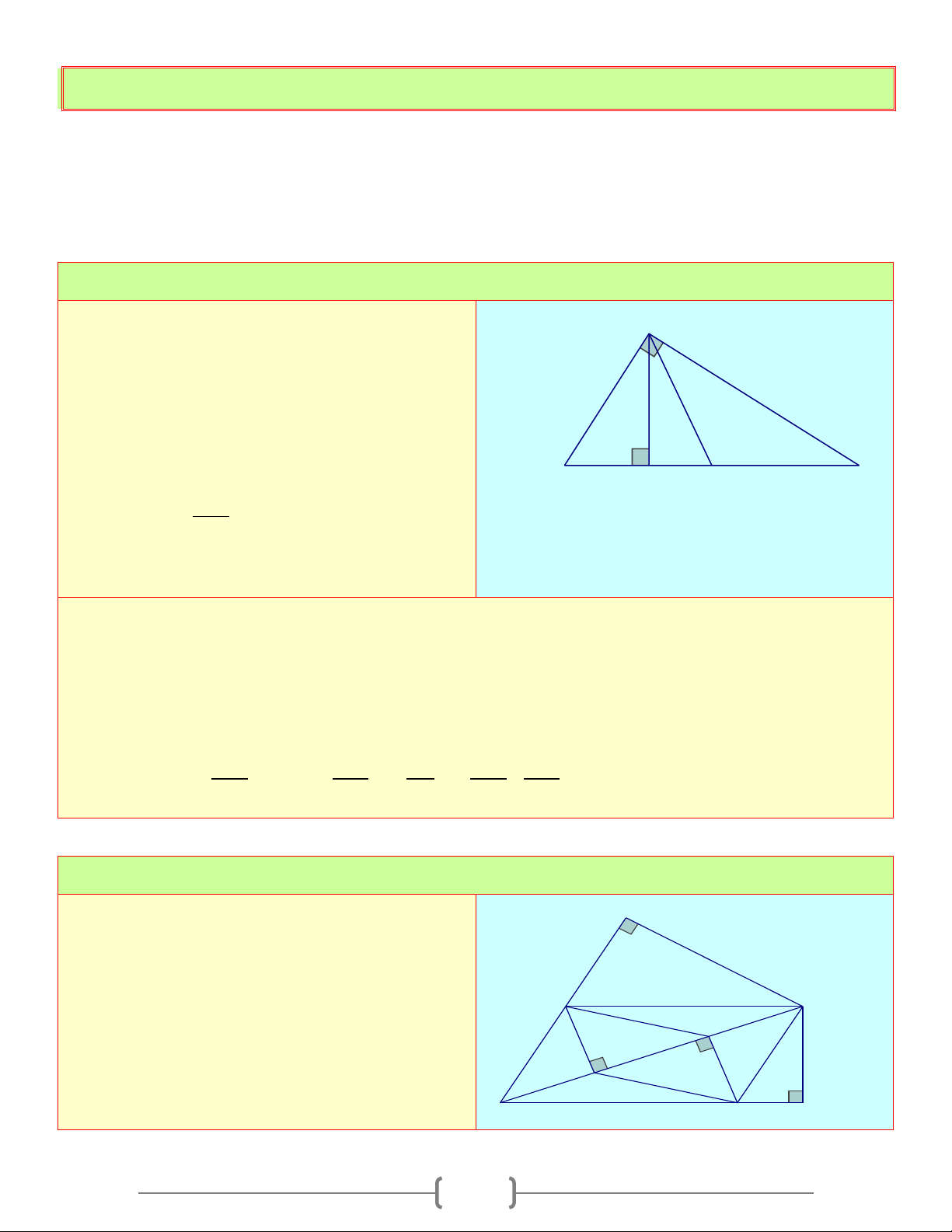
Tính diện tích tam giác có độ dài ba cạnh là A 10c , m 17c , m 21cm 17 10 B H C 21 12 Lời giải Xét A
∆ BC có AB =10c , m BC = 21c , m CA =17cm Kẻ đường cao 1 1
AH ⊥ BC ⇒ S = AH BC = AH ABC . .21. 2 2
Gọi BH = x(cm)(x > 0) thì HC = 21− x
Áp dụng hệ pytago cho hai tam giác vuông ABH, AHC ta được: 2 2 2 2 2
AH = AB − BH = − x ( ) 2 2 2 2 10
1 ; AH = AC − CH =17 − (21− x)2 (2)
Từ (1)(2) suy ra: 2 −( − x)2 2 2 17 21
= 10 − x ⇒ 42x = 252 ⇒ x = 6
Thay x = 6 vào (1) ta được: 2 2
AH = 8 ⇔ AH = 8(cm)( AH > 0) Vậy 1 S = = cm . ABC .21.8 84( 2 ) 2
BÀI TẬP TỰ LUYỆN Bài 1: Cho A
∆ BC vuông tại A , đường cao AH A
a) Biết AB = 3c ,
m AC = 4cm . Tính BH,CH, AH và BC
b) Biết BH = 9c , m CH =16cm. B H C
Tính AB, AC, BC, AH Lời giải
a) Dùng định lí Pitago tính được BC = 5cm
Áp dụng hệ thức về cạnh và đường cao tính được AH = 2,4c , m BH =1,8c , m CH = 3,2cm
b) Có BC = BH + HC = 9 +16 = 25(cm)
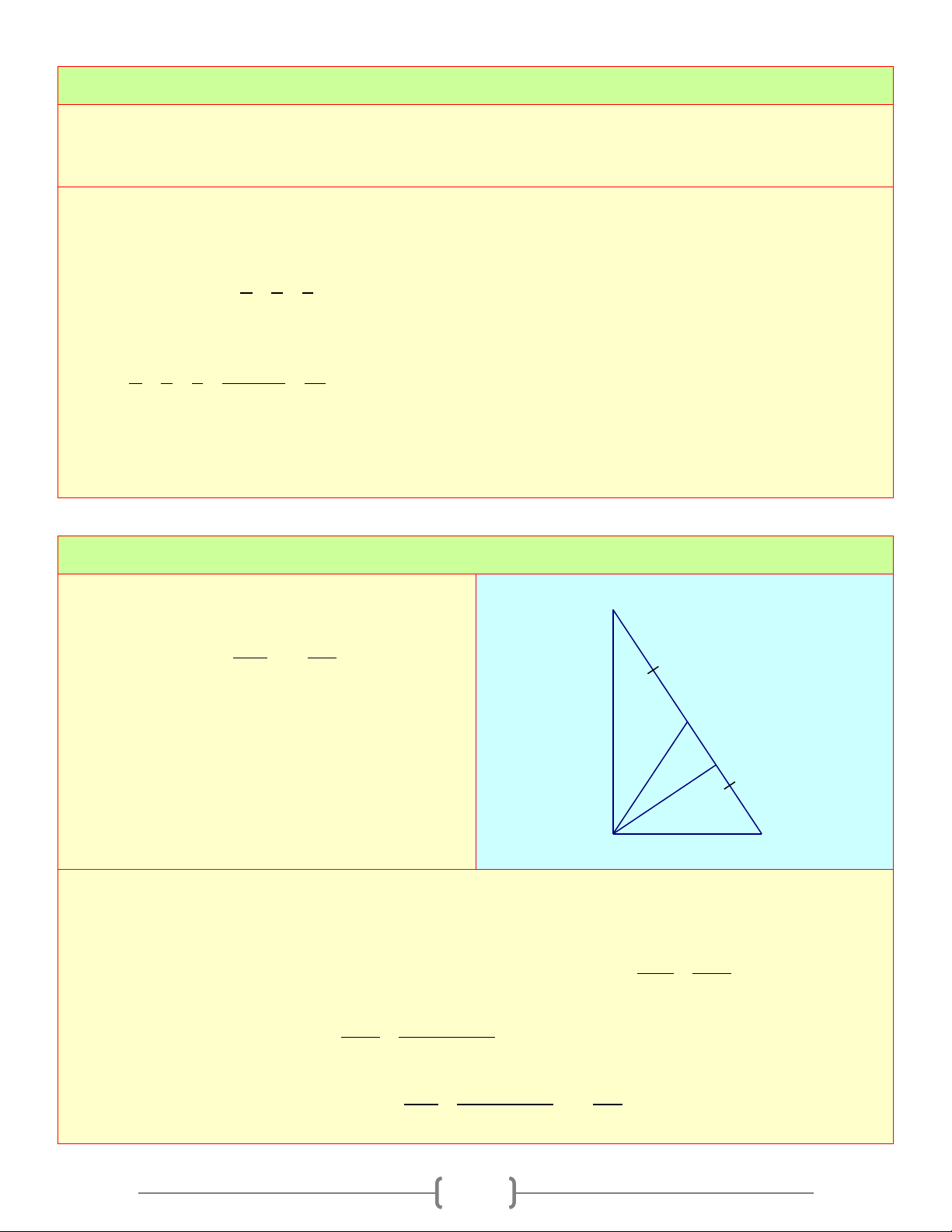
Áp dụng hệ thức về cạnh và đường cao ta tính được AH =15c , m AC = 20cm 13 Bài 2: Cho MN ∆
P có MN = 3c , m NP = 4c , m MP = 5cm M
a) Chứng minh tam giác MNP là tam giác vuông I K
b) Tính đường cao NK
c) Gọi I, H lần lượt là hình chiếu của K trên
MN, NP . Tính IK, HK N H P Lời giải
a) Dùng định lí Pitago đảo, chỉ ra MN ∆
P vuông tại N b) MN ∆
P vuông tại N , đường cao NK . Tính được NK = 2,4cm
c) Tính được MK =1,8c , m KP = 3,2cm MN ∆
K vuông tại K , đường cao KI , tính được KI =1,44cm NKP ∆
vuông tại K , đường cao KK , tính được KK =1,92cm. Bài 3: Cho A
∆ BC vuông tại A , đường cao AH A a) Biết AC 4 AB = 30c , m = . AB 3
Tính AC, BC, AH, BH,CH b) Biết HB 9 B H C AH = 6c , m = . Tính BC HC 16 Lời giải a) AC 4 4
= ⇒ AC = AB = 40(cm) AB 3 3
Áp dụng định lí pitago tính được BC = 50(cm)
Áp dụng hệ thức về cạnh và đường cao, tính được AH = 24c , m BH =18c , m CH = 32cm b) HB 9 9 = ⇒ HB = HC HC 16 16
Áp dụng hệ thức về cạnh và đường cao, 14 có 2 2 9 2 AH = . HB HC ⇒ 6 =
HC.HC ⇒ HC = 64 ⇒ HC = 8(cm) 16
⇒ HB = 4,5(cm) ⇒ BC =12,5(cm). Bài 4: Cho A ∆ BC vuông tại A , có B AB = 6c ,
m AC = 8cm . Các đường phân giác
trong và ngoài góc B cắt đường thẳng AC tại
D và E . Tính AD, AE E A D C Lời giải
Áp dụng định lí Pitago cho A
∆ BC vuông tại A , có 2 2 2
AB + AC = BC ⇒ BC =10(cm) Mặt khác A
∆ BC có phân giác trong AD AB 6 3 AD DC BD ⇒ = = = ⇒ = DC BC 10 5 3 5 Đặt AD DC =
= k (k > 0) ⇒ AD = 3k; DC = 5k 3 5
Mà AD + DC = AC ⇒ 3k + 5k = 8 ⇒ k =1⇒ AD = 3c , m DC = 5cm Hơn nữa A
∆ BC có phân giác ngoài AE AB 3 AE EC BE ⇒ = = ⇒ = EC AC 4 3 4 Đặt AE EC =
= h(h > 0) ⇒ AE = 3 , h EC = 4h 3 4
Mà AE + AC = EC ⇒ 3h +8 = 4h ⇒ h = 8 ⇒ AE = 3.8 = 24(cm) . 15
Dạng 2: Tính chu vi, diện tích các hình Cách giải:
Bước 1: Hình cần tính chu vi, diện tích là hình gì?
Bước 2: Viết công thức tính chu vi, diện tích của hình đó
Bước 3: Tính độ dài các đoạn thẳng chưa biết (đã học ở dạng 1)
Bước 4: Thay số và tính chu vi, diệc tích. Kết luận. Bài 1: Cho A
∆ BC vuông tại A , đường cao A
AH (H ∈ BC) . Biết BH = 9c ,
m CH =16cm . Tính
chu vi và diện tích của A ∆ BC 9 16 B H C Lời giải
Ta có BC = 9 +16 = 25(cm)
Áp dụng hệ thức và cạnh và đường cao cho A
∆ BC vuông tại A , đường cao AH , có: 2
AB = BH.BC = 9.25 ⇒ AB = 9.25 =15(cm) 2
AC = CH.BC =16.25 ⇒ AC = 16.25 = 20(cm) Chu vi của A
∆ BC là AB + BC + CA =15 + 20 + 25 = 60(cm) Diện tích của A ∆ BC là 1 1 A . B AC = .15.20 =150( 2 cm ) 2 2 Bài 2: Cho A
∆ BC vuông tại A , đường cao A
AH (H ∈ BC) . Biết AB = 6c ,
m AH = 4,8cm . Tính
chu vi và diện tích của A ∆ BC 6 4,8 B H C Lời giải 16
Cách 1: Vì AH ⊥ BC nên  0 AHB = 90 Xét A
∆ BH vuông tại H , có 2 2 2
AB = AH + BH (Định lí Pitago)⇒ BH = 3,6(cm) Xét A
∆ BC vuông tại A , đường cao AH , có 2
AH = BH.BC (hệ thức giữa cạnh và đường cao) 2 2 AB 6 ⇒ BC = = = 10(cm) BH 3,6 Hơn nữa 2 2 2
AB + AC = BC (Định lí Pitago) 2 2 2 2 2
AC = BC − AB =10 − 6 = 64 ⇒ AC = 8(cm) Chu vi của A
∆ BC là AB + BC + CA = 6 + 8 +10 = 24(cm) Diện tích của A ∆ BC là 1 1 A . B AC = .6.8 = 24( 2 cm ) 2 2 Cách 2: Xét A
∆ BC vuông tại A , đường cao AH , có 1 1 1 1 1 1 = + ⇒ = + ⇒ AC = 8 cm 2 2 2 2 2 2 ( ) AH AB AC 4,8 6 AC 2 2 2 2 2
⇒ AC = BC − AB =10 − 6 ⇒ AC = 8(cm) Chu vi của A
∆ BC là AB + BC + CA = 6 + 8 +10 = 24(cm) Diện tích của A ∆ BC là 1 1 A . B AC = .6.8 = 24( 2 cm ) 2 2 Bài 3: Cho A
∆ BC có AC = 5c , m BC = 7cm A
a) Gọi H là hình chiếu của A trên BC và biết 5
HC = 4cm . Tính AH và diện tích A ∆ BC K
b) Gọi K là hình chiếu của H trên AC . Tính
chu vi tứ giác ABHK B H 7 C Lời giải
a) Vì H là hình chiếu của A trên BC nên AH ⊥ BC tại H ⇒  =  0 AHB AHC = 90 Xét A
∆ HC vuông tại H có 2 2 2
AC = AH + HC ⇒ AH = 3(cm) 17 1 1 S = AH BC = = cm ABC . .3.7 10,5( 2 ) 2 2
b) Có BH = BC − HC = 7 − 4 = 3(cm) Xét A
∆ HB vuông tại H có 2 2 2
AB = AH + BH ⇒ AB = 3 2 (cm)
Vì K là hình chiếu của H trên AC nên HK ⊥ AC tại ⇒  =  0 K AKH CKH = 90 Xét A
∆ HC vuông tại H , đường cao HK có 2 2 2
AH = AK.AC ⇒ AK = AH : AC = 3 :5 =1,8(cm)
⇒ KC = AC − AK = 5 −1,8 = 3,2(cm) Hơn nữa 2
HK = AK.KC =1,8.3,2 = 5,76 ⇒ HK = 2,4(cm)
Vậy chu vi của tứ giác ABHK là AB + AK + HK + HB = 3 2 +1,8+ 2,4 + 3 ≈11,443(cm) . Bài 4: Cho A
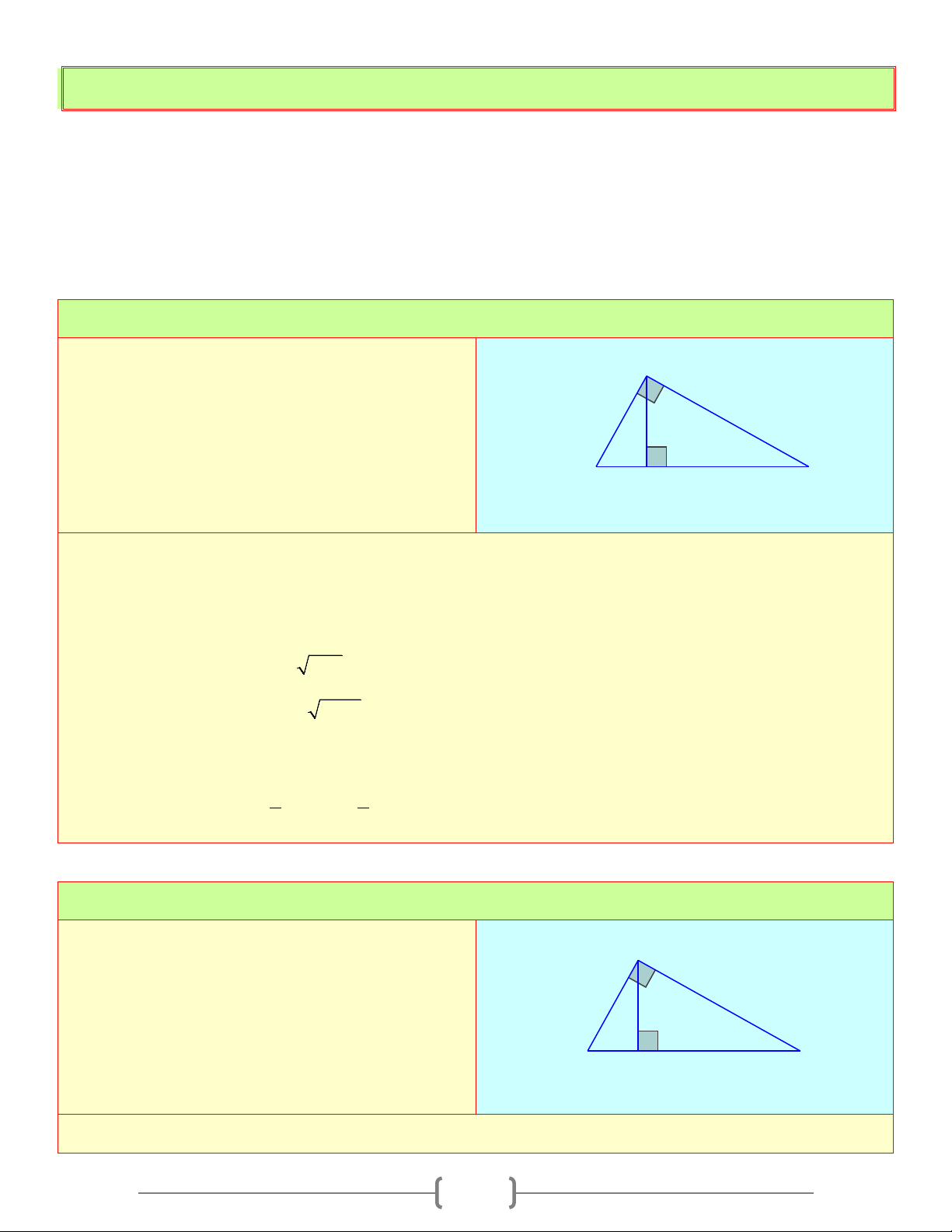
∆ BC vuông tại C , đường cao CH . Biết C AC =15c ,
m BH =16cm . Tính diện tích A ∆ BC . 15 x A H 16 B Lời giải
Đặt AH = x(cm), x > 0 ⇒ AB = x +16(cm) Xét A
∆ BC vuông tại C , đường cao CH có 2
AC = AH.AB (hệ thức về cạnh và đường cao) 2
⇒15 = x(x +16) ⇔ (x −9)(x + 25) = 0 ⇔ x = 9 (thỏa mãn) Vậy AH = 9c ,
m AB = 9 +16 = 25(cm) Hơn nữa 2
CH = AH.HB = 9.16 ⇒ CH = 9.16 =12(cm) Diện tích A ∆ BC là 1 1
CH.AB = .12.25 =150( 2 cm ) . 2 2 18 Bài 5:
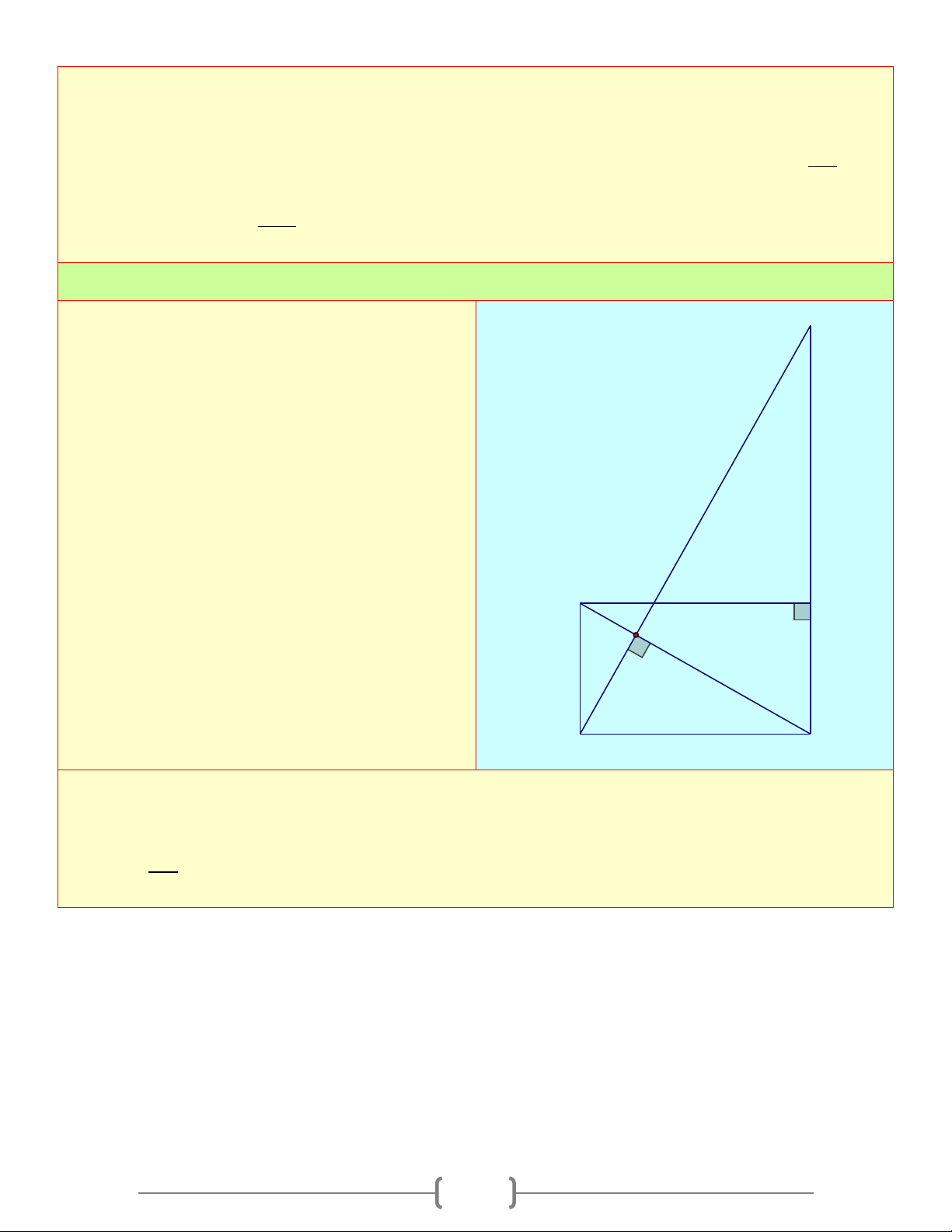
Cho hình thang ABCD( AB / /CD) , hai đường A B
chéo AC và BD vuông góc nhau tại O O a) Chứng minh 1 S = AC BD ABCD . 2
b) Biết BD = 5c ,
m đường cao BH = 4cm . Tính D H C E
diện tích hình thang ABCD Lời giải a) Ta có 1 1 1 S = S + S
= AO BD + CO BD = BD AO + CO = BD CO ABCD ABD BDC ( ) 1 . . . 2 2 2 2
b) Kẻ BE / /AC (E ∈ DC)
mà AB / /CD, E ∈ DC ⇒ AB / /CE do đó tứ giác ABEC là hình bình hành (dấu hiệu nhận biết)
⇒ AC = BE (tính chất hình bình hành) Xét B
∆ HD vuông tại H có 2 2 2
BD = BH + HD (Pitago) 2 2 2
⇒ 5 = 4 + HD ⇒ HD = 3(cm)
Vì BD ⊥ AC và AC / /BE ⇒ BD ⊥ BE ⇒  0 DBE = 90 Xét DB ∆
E vuông tại B , đường cao BH có 2 2 16 BH = .
HD HE ⇒ 4 = 3.HE ⇒ HE = (cm) 3 2
BE = HE (HD + HE) 16  16  400 20 . = . 3+ = ⇒ BE =   (cm) 3  3  9 3 Do đó 20 AC = (cm). Vậy 1 20 50 S = = cm . ABCD . .5 ( 2) 3 2 3 3 Bài 6: Cho A
∆ BC vuông tại A , đường cao A
AH (H ∈ BC) , biết AB 20 =
; AH = 420(cm) , AC 21 16 Tính chu vi A ∆ BC ? 12 B H D C 19 Lời giải Ta có: AB 20 AB AC = ⇒ =
= k(k > 0) ⇒ AB = 20k; AC = 21k AC 21 20 21
Áp dụng hệ thức lượng trong tam giác vuông, ta có: 2 2 2
AH.BC = A .
B AC ⇒ 420.BC = 20.21.k = 420k ⇒ BC = k Lại có:  = BC 29k 2 2 2 2 2 2 2 2
BC = AB + AC = 400k + 441k = 841k = (29k) ⇒ 
⇒ k = 29k ⇔ k = 29 2 BC = kAB = 580(cm) 
⇒ AC = 609(cm) ⇒ P = cm ABC 2030( ) BC =  841(cm)
BÀI TẬP TƯƠNG TỰ Bài 1: Cho MN ∆
P vuông tại M , MN =12c , m NP =13cm M , đường cao MK
a) Tính MK,MN, KP 12
b) Tính diện tích MN ∆ P N K 13 P Lời giải
a) Áp dụng định lí Pitago, tính được MP = 5(cm)
Áp dụng hệ thức về cạnh và đường cao, tính được 60 MK = (cm) 144 NK = (cm) 25 , , KP = (cm) 13 13 13 b) S = cm MNP ( 2 30 ) Bài 2:
Tính diện tích tam giác ABC có A AB =10c , m AC =17c , m BC = 21cm 10 17 B H C 20 Lời giải
Kẻ AH ⊥ BC tại H vàv đặt BH = x(cm), x > 0 ⇒  =  0
AHB AHC = 90 và HC = 21− x(cm) Hơn nữa  =  0 AHB AHC = 90 Xét A
∆ HB vuông tại H có 2 2 2 2 2 2
AB = AH + BH ⇒ AH = AB − BH ( )1 Xét A
∆ HC vuông tại H có 2 2 2 2 2 2
AC = AH + CH ⇒ AH = AC − CH (2) Từ (1)(2) suy ra 2 2 2 2 2 2 2
AB − BH = AC − CH ⇔ 10 − x =17 − (21− x)2 ⇔ x = 6 (thỏa mãn)
Vậy BH = 6(cm) Ta có 2 2 2 2 2
AH = AB − BH =10 − 6 = 64 ⇒ AH = 8(cm) Vậy 1 1 S = AH BC = = cm . ABC . .8.21 84( 2 ) 2 2 Bài 3:
Cho hình thang ABCD có  =  0 =  0 A D 90 , B = 60 D 30cm C CD = 30c ,
m CA ⊥ CB . Tính diện tích hình thang y ABCD x 600 A B Lời giải
a) Cách 1: Dùng phương pháp đại số hóa Ta có  0 = −  0 0 0 CAB 90
ABC = 90 − 60 = 30 ( ) 1
Hình thang ABCD có  =  0 = ⇒ ⇒  =  A D 90 DC / / AB DCA CAB (2) Từ (1)(2) suy ra  0 DCA = 30
Đặt AD = x(cm), x > 0 Xét A
∆ DC vuông tại D có  0 1
DCA = 30 ⇒ AD = AC ⇒ AC = 2AD = 2x(cm) 2 Hơn nữa 2 2 2
AC = AD + DC ⇒ ( x)2 2 2 2 2
= x + 30 ⇒ x = 300 ⇒ x = AD =10 3 (cm) 21
⇒ AC = 2x = 20 3 (cm)
Đặt BC = y(cm), y > 0 Xét A
∆ BC vuông tại C , có  0 1
CAB = 30 ⇒ BC = AB ⇒ AB = 2BC = 2y (cm) 2 Lại có 2 2 2
AB = AC + BC ⇒ ( y) = ( )2 2 2 2 2
20 3 + y ⇒ y = 400 ⇒ y = BC = 20(cm)
⇒ AB = 2BC = 40(cm)
( AB +CD).AD (30+ 40).10 3 S = = = cm ABCD 350 3 ( 2 ) 2 2
b) Cách 2: Chỉ ra AC = 2AD
Tính được AD =10 3(cm)
Kẻ CH ⊥ AB tại H
Chỉ ra được ADCH là hình chữ nhật⇒ CH = AD =10 3(cm), HA = CD = 30(cm) 2 Hơn nữa 2 = . CH CH HA HB ⇒ HB =
= 10(cm) ⇒ AB = HA + HB = 40(cm) HA Tính được S = cm . ABCD ( 2 350 3 ) 22
Dạng 3: Chứng minh các hệ thức liên quan đến tam giác vuông
Cách giải: Sử dụng các hệ thức về cạnh và đường cao một cách hợp lý theo 3 bước:
Bước 1: Chọn các tam giác vuông thích hợp chứa các đoạn thẳng có trong hệ thức
Bước 2: Tính các đoạn thẳng đó nhờ hệ thức về cạnh và đường cao
Bước 3: Liên kết các giá trị trên để rút ra hệ thức cần chứng minh. Bài 1: Cho A
∆ BC vuông tại A , đường cao AH . A Chứng minh rằng: a. 2 2 2 2
AB + CH = AC + BH
b. Vẽ trung tuyến AM của A ∆ BC . Chứng minh rằng: B H M C 2 +) 2 2 BC 2 AB +AC = + 2AM 2 +) 2 2
AC − AB = 2.BC.HM ( AC > AB) Lời giải
a) Xét tam giác vuông HAB và tam giác vuông HAC , theo định lý pytao ta có: 2 2 2 2 2
AB − BH = AH = AC − HC ⇒ đpcm
b) Áp dụng định lý pytago vào tam giác vuông ABC , ta có: 2 2 2 2 2 2 2 2 BC 2 BCBC BC BC 2
AB + AC = BC ; + 2AM = + 2 = + =   BC ⇒ đpcm 2 2  2  2 2 Bài 2:
Cho hình bình hành ABCD có góc nhọn A . M
Gọi I, K lần lượt là hình chiếu của B,D trên
đường chéo AC . Gọi M, N là hình chiếu của B C
C trên các đường thẳng AB, AD . Chứng minh K rằng: I a. AK = IC A D N 23
b. Tứ giác BIDK là hình bình hành c. 2 AC = A . D AN + A . B AM Lời giải
a) Ta có: AK = AI + IK;IC = IK + KC ⇒ AK = IC (đpcm)
b) Xét tứ giác BIDK, có: BI // DK
⇒ ◊BIDK là hình bình hành. BI = KD c) Ta có: 2 A ∆ KD# A
∆ NC(g.g); A ∆ BI# A
∆ CM (g.g) ⇒ AC = A . D AN + A . B AM (đpcm). Bài 3:
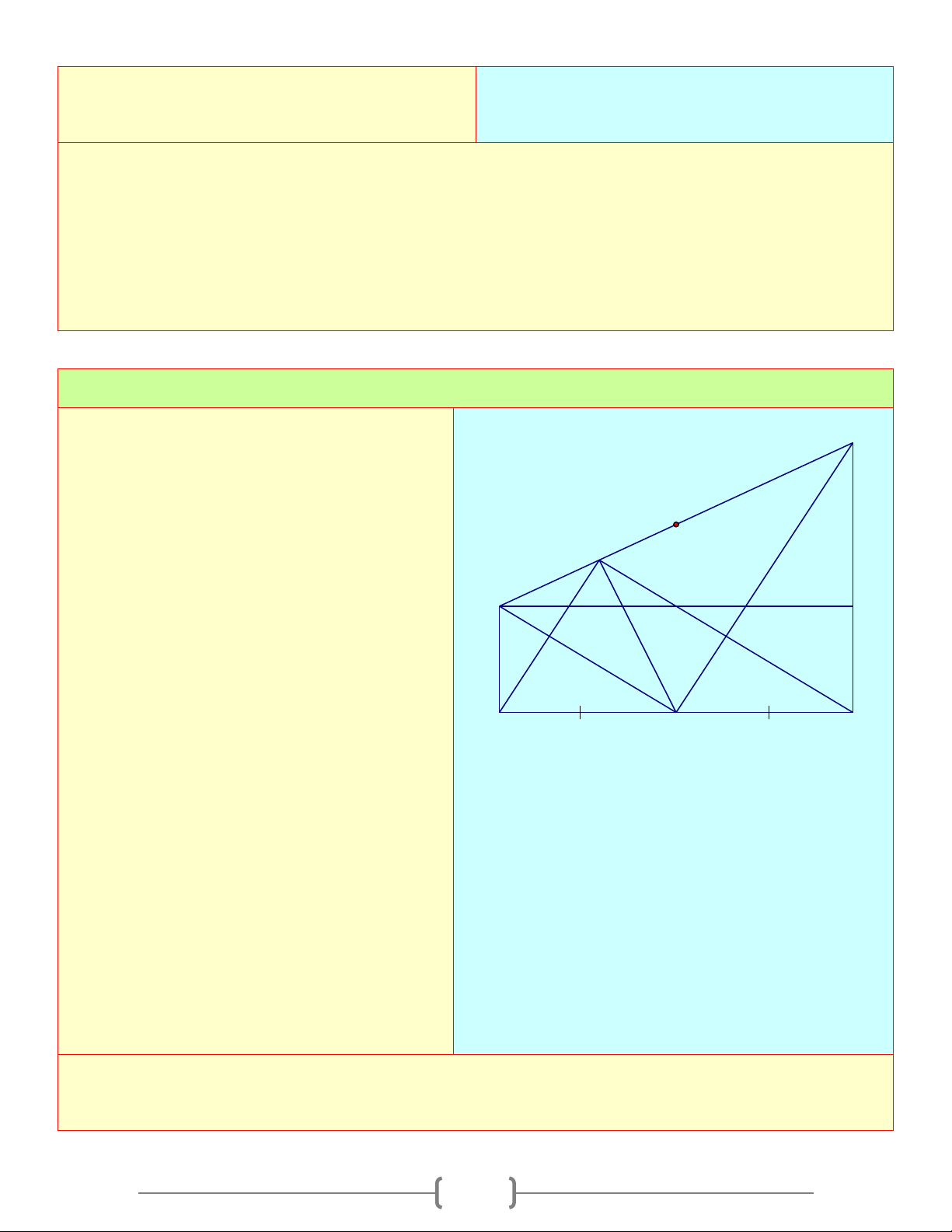
Cho AB = 2a cố định. O là trung điểm của D
AB , về cùng một phía của AB ta vẽ hai tia
Ax, By , trong đó AB ⊥ By, AB ⊥ Ax . Lấy
điểm C thuộc Ax , D thuộc By sao cho I  0
COD = 90 ( AC ≤ BD) . Hạ OM vuông góc M
với CD , nối OC cắt AM tại E , nối OD cắt C 1 H 2 BM tại F .
a. Chứng minh CO và DO là phân giác của f 2   1 AC ; D BCD A O B
b. Chứng minh tam giác MAB vuông tại M
c. Chứng minh tứ giác OEMF là hình chữ nhật
d. OE.OC = OF.OD
e. Cho C và D chuyển động mà  0 COD = 90
. Chứng minh AC.BD không đổi f. Cho  0
MBA = 30 . Tính AC và BD theo a
g. Xác định vị trí của C để cho:  tanCDB = 3 Lời giải
a. Từ giả thiết suy ra AC / /BD vì cùng ⊥ AB 24
Tứ giác ABCD là hình thang.
Gọi I là trung điểm của CD ⇒ OI là đường trung bình của hình thang ABCD ⇒ ⇒  =  OI / / AC IOC C (so le trong) 2 Ta có C
∆ OD vuông tại O (giả thiết) = ⇒ = ⇒=  =  =  IC ID IO IC
IOC C C ⇒ CO là phân giác  ACD 1 2
Tương tự: DO là phân giác của góc  BDC
b) Theo tính chất đường phân giác 1
⇒ OM = OA = OB ⇒ MO = AB ⇒ M
∆ AB vuông tại M 2 c) O
∆ MC vuông tại M và OA ∆
C vuông tại A , mà  = 
C C (chứng minh trên) 1 2   =   =  MOC AOC C C ⇒ 
⇒ OC ⊥ AM = E 1 2 OM  = OA  (cmt) d) + e). Ta có:  =  0 AO AC 2
AOC BOD = 90 ⇒ A ∆ OC# B ∆ DO ⇒ =
⇒ AC.BD = A . O BO = a BD BO
f) Ta có: OC / /MB(⊥ AM ) ⇒  =  0 O MBO = 30 1 0 1 a 2 ⇒ AC = 0. A tan30 = . a =
; AC.BD = a ⇒ BD = a 3 3 3
g) Hạ CH ⊥ BD, đặt AC = x(x > 0)
Tứ giác ACHD là hình chữ nhật ⇒ BH = ;xCH = AB = 2a Ta có  CH CH 2a 2 = 3 ⇔ = 3 a tanCDB ⇔ DH = = ⇒ BD = + x HD 3 3 3 Theo chứng minh trên: 2
AC.BD = a 2 2 2  2a    2 2 2ax 2 2 a a 2 a a 2 10ax. x  
  a x
a x  2x.   a   (x  )  (x,a  0)  3  3 3 9 9 3 9 a a 10  x   3 3 a( 10  1) a( 10  1)  x   AC  . 3 3 25 Bài 4:
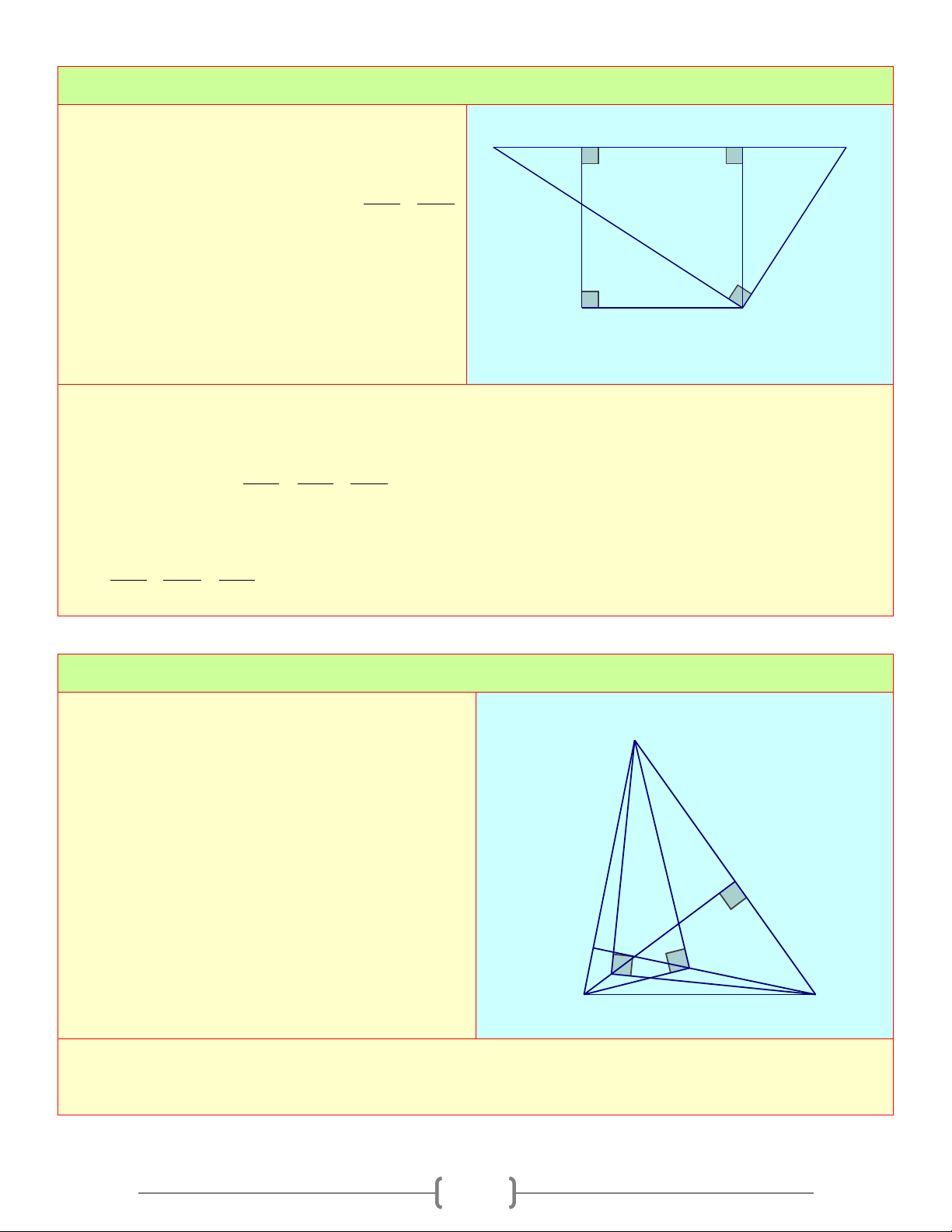
Cho hình vuông ABCD , một điểm E bất kỳ F B C
thuộc cạnh AB . Gọi F là giao điểm của DE P
Và BC . Chứng minh rằng: 1 1 + 2 2 DE DF E không đổi. 2 3 1 A D Lời giải
Dựng qua D đường thẳng vuông góc với DE cắt BC tại P Tam giác DPF , có: 1 1 1 = +
, mà CD = DA ;  = 
D D (cùng phụ với  D ) 2 2 2 CD DP DF 1 2 3 ⇒ DA ∆ E = DC ∆
P ⇒ DE = DP Vậy 1 1 1 + = (đpcm). 2 2 2 DE DF DA Bài 5:
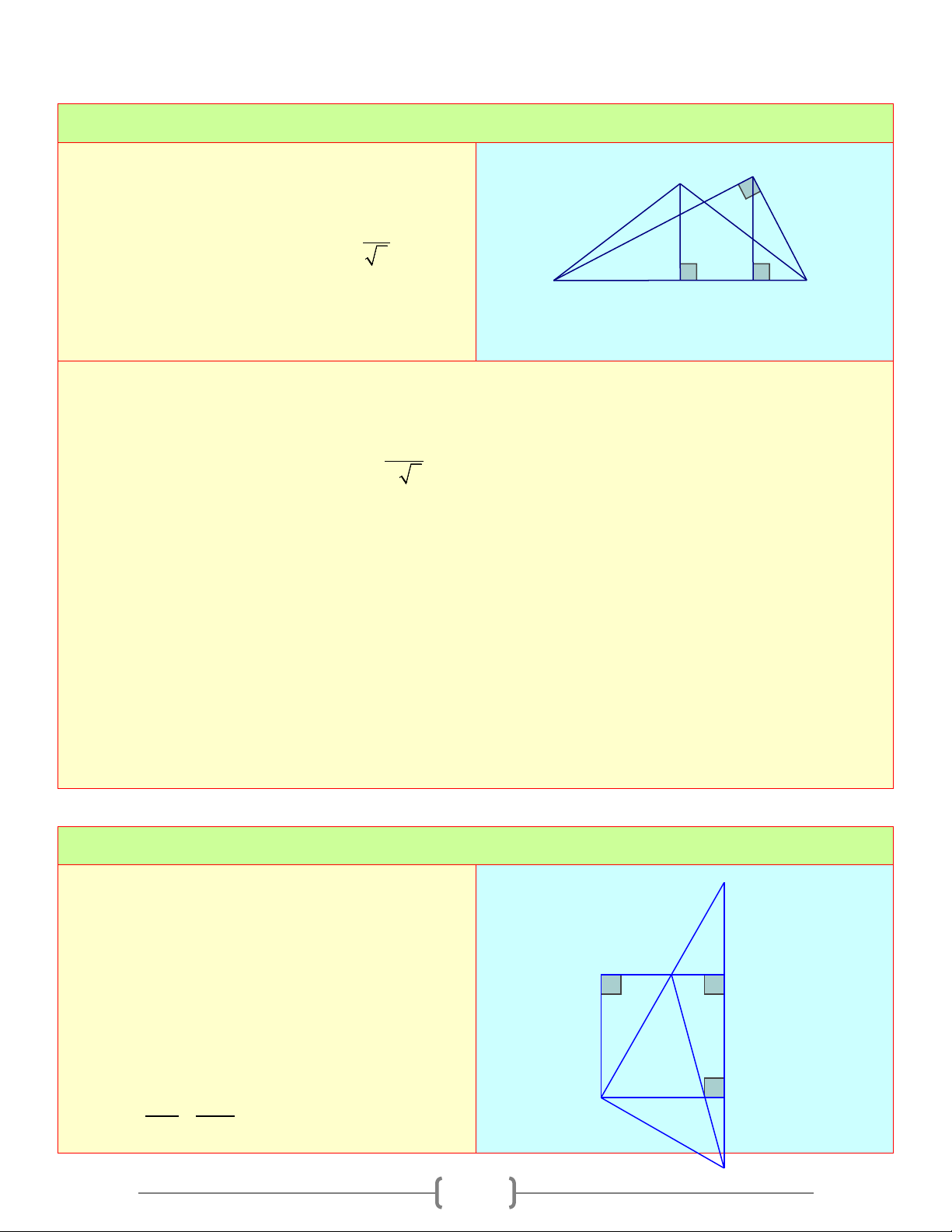
Cho tam giác nhọn ABC , BD và CE là hai A
đường cao. Các điểm N,M trên các đường
thẳng BD,CE sao cho  =  0 AMB ANC = 90 . Chứng minh rằng A ∆ MN cân. D E M N B C Lời giải Xét A ∆ BD và A ∆ CE có: 26   =  0 : ; = 90 AB AD BAD chung ADB AEC ⇒ A ∆ BD# A ∆ CE ⇒ =
⇒ AE.AB = A . D AC ( ) 1 AC AE A
∆ MB vuông tại M (gt), ME là đường cao, theo hệ thức liên quan tới đường cao có: 2
AM = AE.AB(2) . Tương tự ta có: 2 AN = A . D AC (3) Từ (1)(2)(3) có: 2 2
AM = AN ⇒ AM = AN ⇒ A ∆ MN cân. Bài 6:
Cho đoạn thẳng AB = 4cm . C là điểm di động M
sao cho BC = 3c .
m Vẽ tam giác AMN vuông
tại A có AC là đường cao. Xác định vị trí điểm C để 1 1 +
đạt giá trị lớn nhất. 2 2 AM AN C A B N Lời giải Xét A
∆ MN vuông tại A , AC là đường cao (gt)
Theo hệ thức liên quan đường cao trong tam giác vuông, ta có: 1 1 1 + = 2 2 2 AM AN AC Xét ba điểm ,
A B,C ta có: AC ≥ AB − BC ; AC ≥1(cm) Do vậy: 1 1 ≤ 1 ⇔
≤ 1, dấu “=” xảy ra khi và chỉ khi C nằm giữa A và B 2 AC AC
Vậy khi C nằm giữa A và B sao cho BC = 3cm thì 1 1 +
đạt giá trị lớn nhất. 2 2 AM AN 27 Bài 7: Cho A
∆ BC có ba cạnh tỉ lệ với 3,4,5 và chu vi tam giác đó là 48(cm) . Chứng minh rằng A ∆ BC vuông Lời giải
Gọi a,b,c là độ dài ba cạnh của A ∆ BC a b c
Theo đề bài ta có:  = = 3 4 5
a +b +c = 48
Ta có: a b c a + b + c 48 = = = =
= 4 ⇐ a =12;b =16;c = 20 3 4 5 12 12 2 2 2 2
a + b =12 +16 =  400( ) 1 Lại có: 2 2 2 
⇒ c = a + b ⇒ A ∆ BC vuông. 2 2 c = 20 = 400  (2) Bài 8: Cho A
∆ BC cân tại A  ( 0
A < 90 ), kẻ BM ⊥ CA . E 2
Chứng minh rằng: AM 2 AB  = −   1 MCAC  A M B C Lời giải
Lấy E đối xứng với C qua A thì B
∆ CE vuông tại B 2 2
Áp dụng hệ thức về cạnh 2
b' = b'.a ta được: 2 = . BC BC BC MC ME ⇒ MC = = ( )1 CE 2AC 2 2 2 Mặt khác BC 2AC − BC
AM = AC − CM = AC − = (2) 2AC 2AC 2 2 2
Chia (1) cho (2) theo từng vế ta được: AM 2AC − BC 2 AC  = = −   1 (đpcm). 2 MC BCBC  28 Bài 9: Cho A
∆ BC vuông tại A với đường cao AH . D A
Trên nửa mặt phẳng bờ BC có chứa điểm A
lấy điểm D sao cho AB DB = DC = . Chứng 2
minh rằng BD, DH và HA là độ dài ba cạnh B O H C của một tam giác vuông. Lời giải
Gọi O là trung điểm của BC
Đặt OB = OC = R > 0 , do AB DB = DC =
(gt) ⇒ DO là đường trung trực của đoạn BC hay R 2 DOC ∆ vuông tại . O
Gọi HC = x ⇒ OH = RR − ;xBH = 2R − x
Áp dụng hệ thức pytago vào DOC ∆ và DOH ∆
vuông tại O, ta được: 2 2 2 2 2
DC = OC + DO = R + DO ( ) 2 2 2 2
DH = DO + OH = DO + (R − x)2 2 2 2 ;
⇒ DO = DH − (R − x)2 (3)
Thế (3) vào (2) ta được: 2 2 2 2 2 2 2
DC = R + DH − R + 2Rx − x = DH + AH (4) Lại có 2 2 2
DC = DB ⇒ BD = DH + AH ⇒ BD, DH, HA là độ dài ba cạnh của một tam giác vuông
(theo định lý Pytago đảo). Bài 10:
Cho hình vuông ABCD . Gọi I là một điểm K
nằm giữa A và B . Tia DI và tia CB cắt nhau
ở K . Kẻ đường thẳng qua D , vuông góc với A I B
DI . Đường thẳng này cắt đường thẳng BC tại
L . Chứng minh rằng
a) Tam giác DIL là tam giác cân 1 2 C b) Tổng 1 1 +
không đổi khi I thay đổi D 3 2 2 DI DK L 29 trên cạnh AB . Lời giải
a) Tứ giác ABCD là hình vuông (giả thiết)
⇒ AD = CD và  =  0
ADC DCB = 90 (tính chất hình vuông) Lại có  +  0 = ⇒  0 DCL DCB 180 DCL = 90 Mặt khác  +  =  0 =  +  =  0 D D ADC 90 ; D D
IDL = 90 DL ⊥ DI ⇒ D = D (phụ  D ) 1 2 3 2 ( )   3 1 2  =  0 DAI DCL = 90  Xét  A ∆ DI và C
∆ DL , có AD = DC  ⇒ A ∆ DI = C
∆ DL(gcg) ⇒ DI = DL ⇒ DI
∆ L cân tại D  =   D D 1 3  b) Xét DK ∆
L vuông tại D , đường cao DC có 1 1 1 + =
(hệ thức cạnh và đường cao) 2 2 2 DL DK DC mà 1 1 1 DI = DL ⇒ + = 2 2 2 DI DK DC
hơn nữa DC là cạnh hình vuông ABCD nên DC không đổi Vậy 1 1 +
không đổi khi I thay đổi trên cạnh AB . 2 2 DI DK Bài 11: Cho MN ∆
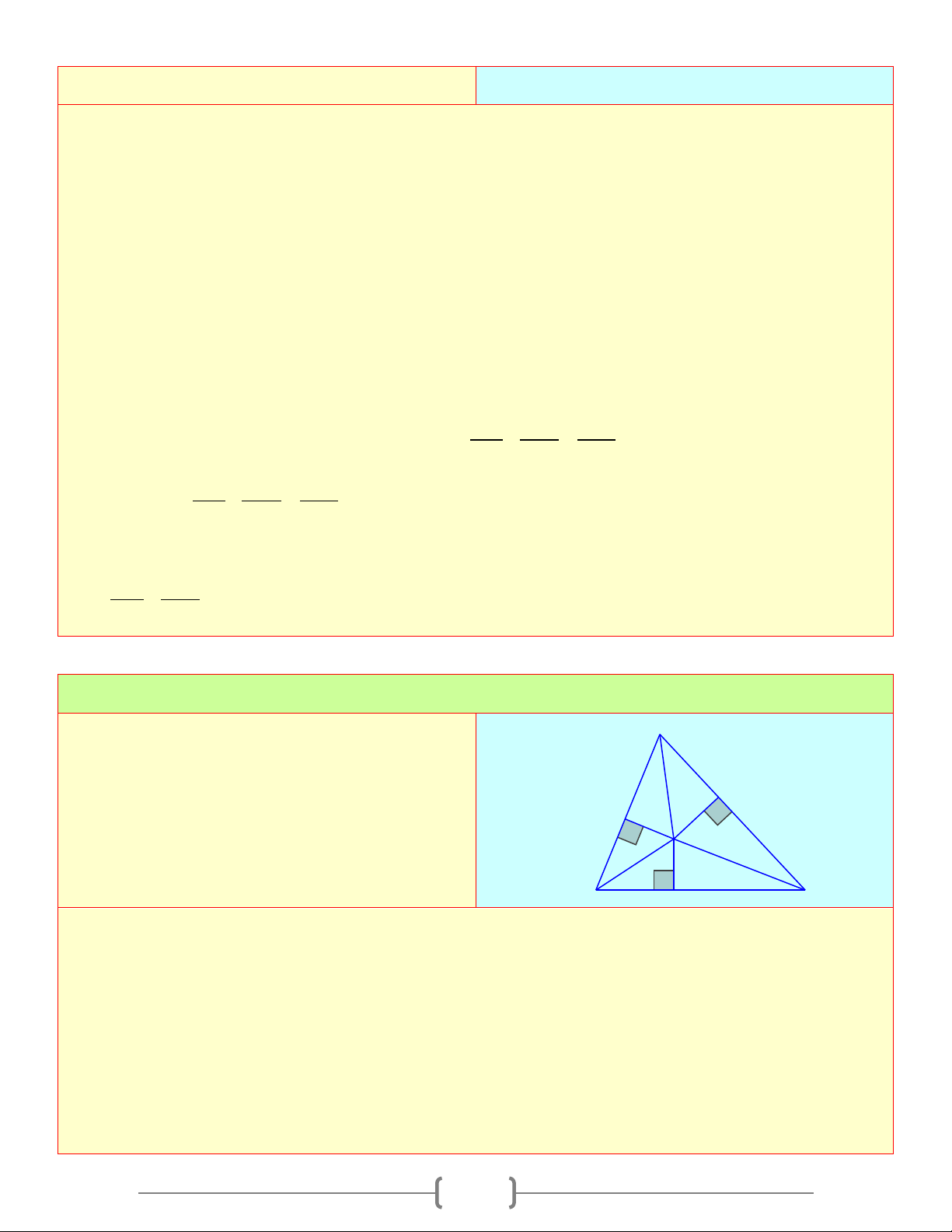
E . Từ một điểm O bất kỳ nằm trong M tam giác kẻ ,
OA OB,OC lần lượt vuông góc C
với MN < NE, EM ( A thuộc MN , B thuộc NE A
, C thuộc EM ). Chứng minh rằng O 2 2 2 2 2 2
MA + NB + EC = AN + BE + CM N B E Lời giải
Ta có OA ⊥ MN tại A ⇒  =  0 OAM OAN = 90
OB ⊥ NE tại ⇒  =  0 B
OBN OBE = 90 ; OC ⊥ ME tại ⇒  =  0 B OCE OCM = 90
Áp dụng định lí Pitago cho các tam giác vuông OA ∆ M , OB ∆ N, OB ∆ E, OC ∆ E, OC ∆ M , có: 2 2 2 2 2
MO = MA + OA = MC + OC ( ) 1 ; 2 2 2 2 2
NO = OB + NB = OA + AN (2) 2 2 2 2 2
EO = OC + EC = OB + BE (3) 30
Cộng (1)(2)(3) theo vế ta được: 2 2 2 2 2 2 2 2 2 2 2 2
MA + OA + OB + NB + OC + EC = MC + OC + OA + AN + OB + BE 2 2 2 2 2 2
⇒ MA + NB +EC = AN + BE + CM (đpcm). Bài 12: Cho A
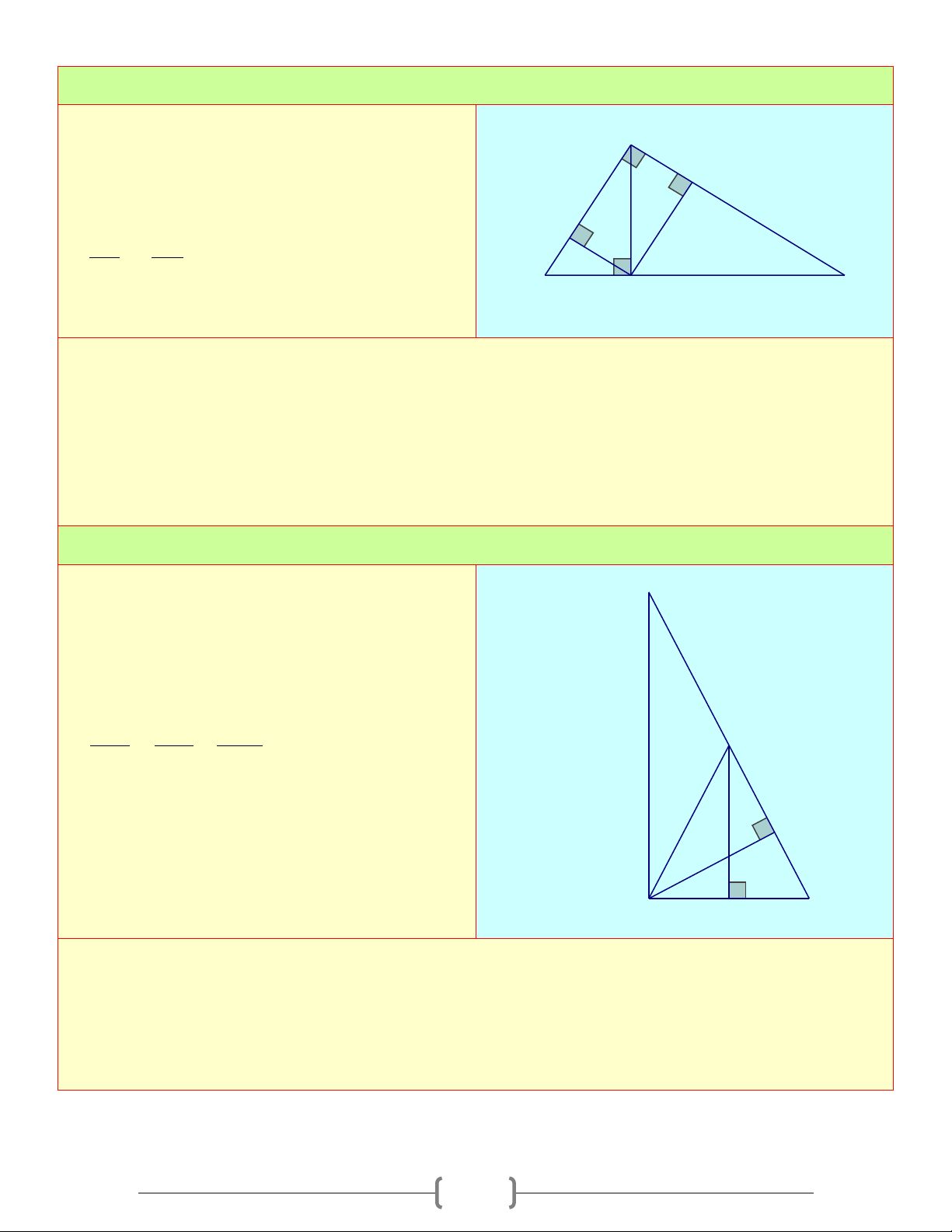
∆ BC vuông tại A , đường cao AH . Gọi B
M , N lần lượt là hình chiếu của H trên M H
AB, AC . Chứng minh rằng
a) AM.AB = AN.AC 2 b) HB AB  A N C = HC AC    c) H . B HC = . MA MB + N . A NC Lời giải
a) Ta có AH là đường cao của A
∆ BC ⇒ AH ⊥ BC tại H ⇒  =  0 AHB AHC = 90
Có M, N lần lượt là hình chiếu của H trên AB, AC ⇒ HM ⊥ AB, HN ⊥ AC tại N Xét A
∆ HB vuông tại H , đường cao HM có 2
AH = AM.AB (1) Xét A
∆ HC vuông tại H , đường cao HN có 2
AH = AN.AC (2)
Từ (1)(2) suy ra AM.AB = AN.AC 2 b) Xét A
∆ BC vuông tại A , đường cao AH có 2 2 AB BH. = . ; = . BC BH AB BH BC AC CH CB ⇒ = = 2 AC CH.CB CH 2
hay HB AB  = HC AC    c) Xét A
∆ HB vuông tại H đường cao HM có 2 HM = . MA MB (3) Xét A
∆ HC vuông tại H đường cao HN có 2 HM = . MA MB (4) Từ (3)(4) 2 2 ⇒ . MA MB + N .
A NC = HM + HN (5) MH ∆ N vuông tại 2 2 2
H ⇒ HM + HN = MN (6) Từ (5)(6) 2 ⇒ . MA MB + N . A NC = MN (7)
Tứ giác AMHN có  =  =  0
AMH ANH MAN = 90 ⇒ ◊AMNH là hình chữ nhật ⇒ AH = MN (8) Xét A
∆ BC vuông tại A , đường cao AH có: 2 AH = . HB HC (9) 31
Từ (7)(8)(9) suy ra H . B HC = . MA MB + N . A NC . Bài 13:
Cho tứ giác ABCD có  +  0 C D = 90 . Chứng E minh rằng 2 2 2 2
AB + CD = AC + BD A B D C Lời giải Vì  +  0 0
C D = 90 <180 nên hai đường thẳng AD và BC cắt nhau
Gọi E là giao điểm của AD và BC Xét DC ∆ E có  +  0 = ⇒  0 C D 90 DCE = 90
Áp dụng định lí Pitago ta có: A ∆ BE vuông tại 2 2 2
E ⇒ AB = AE + BE DC ∆ E vuông tại 2 2 2
E ⇒ DC = DE + CE A ∆ CE vuông tại 2 2 2
E ⇒ AC = AE + CE A ∆ BD vuông tại 2 2 2
E ⇒ BD = DE + BE Do đó 2 2 + = ( 2 2 + )+( 2 2 + ) = ( 2 2 + )+( 2 2 + ) 2 2 AB CD AE BE DE CE AE CE BE
DE = AC + BD . Bài 14:
Cho hình chữ nhật ABCD có AB = 2AD . Trên cạnh lấy điểm A
E bất kì. Tia AE cắt đường B
thẳng CD tại F Chứng minh rằng E 1 1 1 = + 2 2 2 AB AE 4AF H D C F x Lời giải 32
Kẻ tia Ax ⊥ AF tại A , cắt đường thẳng CD tại H Xét A
∆ HF vuông tại A , đường cao AD có 1 1 1 = + (1) 2 2 2 AD AH AF Chỉ ra  = 
HAD EAB (phụ với 
DAE ) dẫn đến A ∆ DH ∽ A ∆ BE (gg) AH AD 1 ⇒ = = ( AB = AD) 1 1 2
⇒ AH = AE; AD = AB (2) AE AB 2 2 2 Từ (1)(2) 1 1 1 4 4 1 1 1 1 ⇒ = + ⇔ = + ⇒ = + . 2 2 2 2 2 2 2 2 2  1   1  AF AB AH AF AB AE 4AFAB   AH 2 2      Bài 15:
Cho hình thoi ABCD có  0
A =120 . Tia Ax tạo A với góc  BAx bằng 0
15 và cắt cạnh BC tại M , B D
cắt đường thẳng DC tại N . Chứng minh rằng M 1 1 4 H E + = . 2 2 2 AM AN 3AB C N Lời giải
Trên cạnh DC lấy điểm E sao cho  0
DAE =15 ⇒  =  −  + 
EAN BAD (DAE BAx) 0 = 90
Kẻ AH ⊥ DC tại H Xét A
∆ EN vuông tại A , đường cao 1 1 1 AH ⇒ + = 1 2 2 2 ( ) AE AN AH D ∆ AE = B
∆ AM (gcg) ⇒ AE = AM (2) A ∆ DC có  =  0
ADC DAC = 60 ⇒ A ∆ DC đều 2 A ∆ DH vuông tại 2 2 2 2 2 2 2  AD  3 2 3 2
H ⇒ AD = AH + DH ⇒ AH = AD − DH = AD − = AD =   AB  2  4 4 1 4 ⇒ = 3 2 2 ( ) AH 3AB 33 Từ (1)(2)(3) suy ra 1 1 4 + = . 2 2 2 AM AN 3AB 34
BÀI TẬP TRẮC NGHIỆM Câu 1: Cho A
∆ BC vuông tại A , đường cao AH , có AB = 9(cm), AC =12(cm). Độ dài ba cạnh
AB, BH,CH lần lượt là:
a) 9,6(cm) b) 6,9(cm)
c) 8,6(cm) d) 6,8(cm) Chọn đáp án A A Giải thích: Ta có:
Áp dụng định lí Pytago vào tam giác ABC 12 9
vuông tại A , ta có: 2 2 2
BC = AB + AC 2 2
= 9 +12 = 225 ⇒ BC =15(cm) B H C
Áp dụng hệ thức lượng trong tam giác vuông ta có: 2 2 81
AB = BC.BH ⇔ 9 =15BH ⇒ BH = = 5,4(cm) 15
Ta có: CH = BC − BH =15−5,4 = 9,6(cm) . Câu 2: Cho OE ∆
F vuông tại O , đường cao OI , có IE = 3(cm), FI =12(cm) . Độ dài đoạn thẳng
OE,OF lần lượt là: a) 3 5 b) 4 5 c) 5 5 d) 6 5 Chọn đáp án D O Giải thích: Ta có:
Áp dụng hệ thức lượng trong tam giác vuông
OEF vuông tại O , đường cao OI , ta có: 2
OE = EF.EI = (3+12).3 = 45 ⇒ OE = 45 = 3 5 (cm) 3 12 E I F 2
OF = EF.FI = (3+12).12 =180
⇒ OF = 180 = 6 5 (cm)
Vậy OE = 3 5 (cm);OF = 6 5 (cm). 35 Câu 3: Cho A
∆ BC vuông tại A , đường cao AI , có AB =13(cm), AI =12(cm) . Diện tích tam giác ABC bằng? a) ( 2 202,6 cm ) b) ( 2 202,7 cm ) c) ( 2 202,8 cm ) d) ( 2 202,9 cm ) Chọn đáp án C A Giải thích: Ta có:
Áp dụng định lí Pytago vào A
∆ BI vuông tại I 13 , ta có: 12 2 2 2 2 2 2
AB = AI + BI ⇒ BI = AB − AI 2 2
= 13 −12 ⇒ BI = 25 = 5(cm). B I C
Theo hệ thức lượng trong tam giác vuông, ta 2 2 có: 2 AB 13
AB = BC.BI ⇔ BC = = = 33,8 cm 2 ( ) BI 5 1 1 S = AI BI = = cm ABC . .12.33,8 202,8( 2 ) 2 2 Câu 4: Cho A
∆ BC vuông tại A , đường cao AH , có 1
AB = AC = 5(cm) . Độ dài đường cao AH 2 bằng a) 5 b) 2 5 c) 3 5 d) 4 5 Chọn đáp án B A Giải thích: Ta có: Ta có: 1
AB = AC = 5 ⇒ AC =10(cm) 2
Áp dụng định lí Pytago vào tam giác vuông ABC , ta có: 2 2 2 2 2
BC = AB + AC = 5 +10 =125 B H C
⇒ BC = 125 = 5 5 (cm)
Tam giác ABC , vuông tại , A có đường cao
AH ⇒ AH.BC = A . B AC 36 A . B AC 5.10 ⇒ AH = = = 2 5 (cm) . BC 2 5 Câu 5: Cho A
∆ BC vuông tại A , biết AB 2
= , BC = 2 13. Độ dài đường cao AH của A ∆ BC AC 3 bằng bao nhiêu? a) 0,3 b) 3,3 c) 3,33 d) 3,03 Chọn đáp án C A Giải thích: Ta có: 2 2 AB 2 = ( ) AB 4 AB 4 1 ⇒ = ⇔ = 2 2 2 2 ( ) AC 3 AC 9 AB + AC 13
Mà AB + AC = BC = ( )2 2 2 2 2 13 = 52 B H C Từ (2), suy ra: 2 AB 4 2 =
⇒ AB =16 ⇒ AB = 4(cm) 52 13 Từ (1), suy ra: 4 2
= ⇔ AC = 6(cm) AC 3 Ta có: A . B AC 12
AH.BC = A . B AC ⇔ AH = = ≈ 3,33 BC 13 Câu 6: Cho A
∆ BC vuông tại A , có AB =18(cm), AC = 24(cm) . Các đường phân giác trong và
ngoài của góc B cắt đường thẳng AC lần lượt tại M, N . Tính độ dài đoạn MN a) 6 b) 7 c) 8 d) 9 Chọn đáp án D B Giải thích: Ta có: Xét A
∆ BC vuông tại A , ta có: 18 2 2 2 2 2
BC = AB + AC =18 + 24 = 900 N A M C
⇒ BC = 900 = 30(cm) 24
Do BM là đường phân giác của  ABC 37 AM AB 18 3 ⇒ = = = MC BC 30 5 AM 3 AM 3 ⇒ = ⇔ = ⇒ AM = 9 AM + MC 3+ 5 24 8  AC
Câu 7: Hình thang ABCD có AB / /CD, hai đường chéo vuông góc. Diện tích hình thang bằng
bao nhiêu biết BD =15cm , đường cao hình thang bằng 12(cm) . a) ( 2 150 cm ) b) ( 2 250 cm ) c) ( 2 105 cm ) d) ( 2 205 cm ) Chọn đáp án A A B Giải thích: Ta có: Kẻ 2 2 2 2 2
BH ⊥ CD ⇒ DH = BD − BH =15 −12 = 81 2 2
= 15 −12 = 81⇒ DH = 9(cm)
Qua B kẻ đường thẳng song song với AC , D H C E
đường thẳng này cắt DC ở E
Xét tam giác DBE vuông tại B , có: 2 2 2 15
BD = DH.DE ⇒15 = 9.DE ⇔ DE = = 25 9
Diện tích hình thang ABCD là:
( AB +CD).BH DE.BH S = = = cm . ABCD 150( 2 ) 2 2
Câu 8: Tam giác MON vuông tại O , đường phân giác của O cắt cạnh huyền MN thành hai
đoạn có đồ dài 45 (cm) và 60 (cm) . Diện tích của MO ∆ N bằng bao nhiêu 7 7 a) ( 2 52 cm ) b) ( 2 53 cm ) c) ( 2 54 cm ) d) ( 2 55 cm ) 38 Chọn đáp án C O Giải thích: Ta có:
Gọi I là giao điểm của tia phân giác của góc
O và cạnh MN , ta có: 45 2 OM IM 7 45 3 M I N = = = = ( ) OM 9 1 ⇒ = 2 ON IN 60 60 4 ON 16 7 2 OM 9 OM 3 ⇒ = ⇒ = 2 2 2 ( ) OM + ON 9 +16 ON 5  2 MN Ta có: 45 60
MN = MI + IN = + = 15(cm) 7 7 Từ (2), suy ra: 3.MN 3.15 OM = = = 9(cm) 5 5 Từ (1), suy ra: 4.OM 4.9 ON = = = 12(cm) 3 3 Do đó 1 1 S = OM ON = = cm . OMN . .9.12 54( 2 ) 2 2
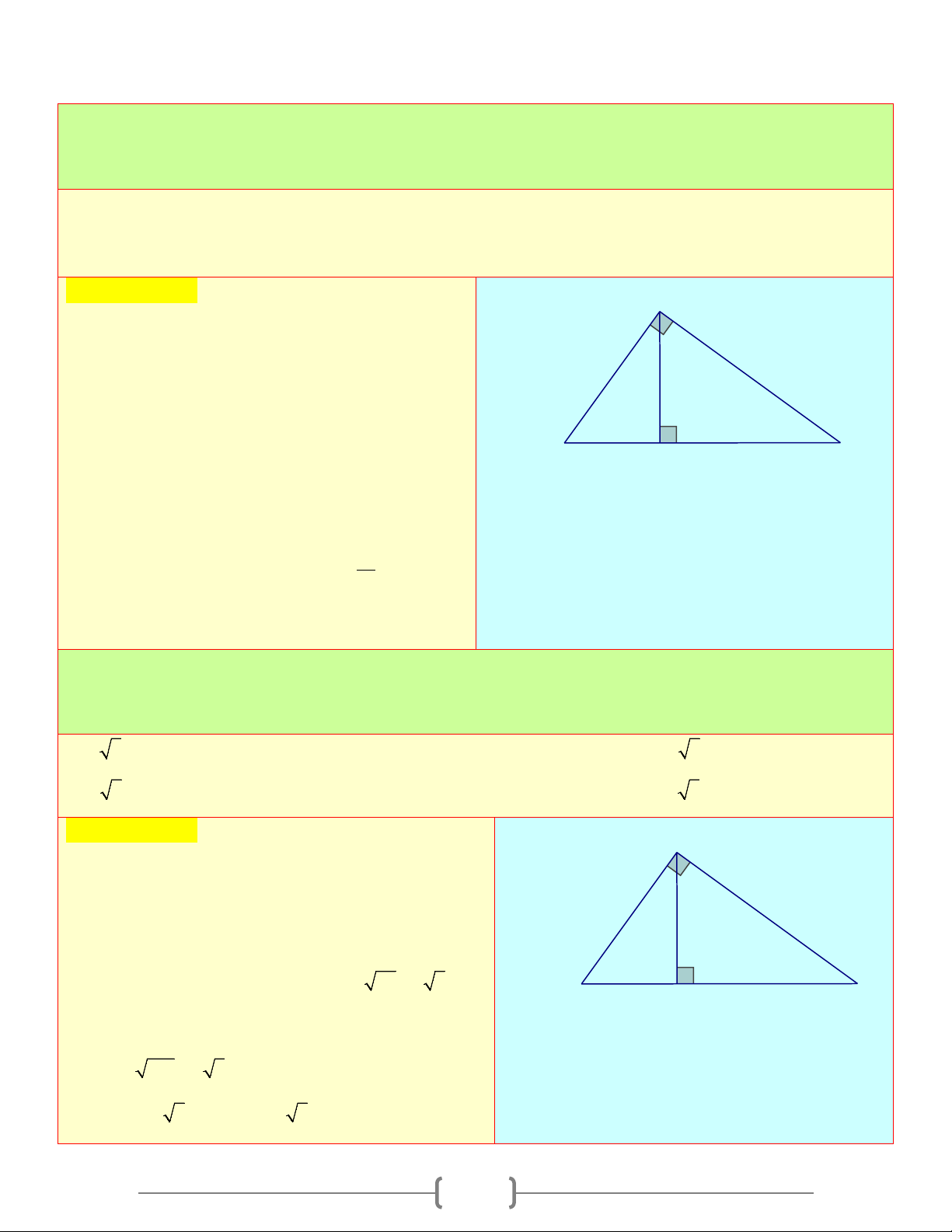
Câu 9: Tam giác ABC vuông tại A , đường cao AH . Khẳng định nào sau đây đúng a) A ∆ HB# C ∆ AB b) A ∆ HC# B ∆ AC c) A ∆ HB# C ∆ HA d) Cả ,
A B,C đều đúng Chọn đáp án D A Giải thích: Ta có: a) A ∆ HB# C ∆ AB(gg) b) A ∆ HC# B ∆ AC (gg) c) A ∆ HB# C ∆ HA(# C ∆ AB) B H C
Câu 10: Tam giác MNP vuông tại M , đường cao MH . Khẳng định nào sau đây sai a) 2 2 MN = . NP NH;MP = . NP PH b) 2
MH = HN.H ;
P MN.MP = N . P MH c) 1 1 1 = + d) ,
A B đúng, C sai 2 2 2 NH MN MP 39 Chọn đáp án D M Giải thích: Ta có: a) 2 2 MN = . NP NH;MP = . NP PH b) 2
MH = HN.H ;
P MN.MP = N . P MH c) 1 1 1 = + N H P 2 2 2 MH MN MP 40 BÀI TẬP VỀ NHÀ Bài 1: Cho A
∆ BC vuông tại A , đường cao AH . A
a. Biết AH = 6c , m BH = 4,5c .
m Tính AB, AC , BC, HC
b. Biết AB = 6c ,
m BH = 3cm . Tính AH và tính
chu vi của các tam giác vuông trong hình vẽ B H C Hướng dẫn giải
a) Tính được: AB  7,5 , cm AC  10 , cm BC  12,5 , cm HC  8cm b) AH  3 3 , cm P  18  6 3 , cm P
 9  3 3cm;P  9  9 3cm ABC ABH ACH Bài 2: Cho A
∆ BC vuông tại A , đường cao AH . A Tính diện tích A
∆ BC , biết AH =12cm BH = 9cm B H C Hướng dẫn giải Ta tính được: 2 S  150cm ABC Bài 3: Cho hình thang A
∆ BC vuông tại A và D . A 15 B
Cho biết AB =15c ,
m AD = 20cm , các đường
chéo AC và BD vuông góc với nhau tại O . 20 Tính
a. Độ dài các đoạn thẳng OB và OD D C
b. Độ dài đoạng thẳng AC
c. Diện tích hình thang ABCD Hướng dẫn giải 41
a) Áp dụng các hệ thức lượng trong tam giác vuông ABD , tính được: BD  2,5 , cm OB  9 , cm OD  16cm
b) Áp dụng các hệ thức lượng trong tam giác vuông DAC tính được: 100 OA =12c ; m AC = (cm) 3 c) Tính được: 1250 S = cm ABCD ( 2) 3 Bài 4:
Cho hình chữ nhật ABCD có AB = 8cm K BC =15cm
a. Tính độ dài đoạn thẳng BD
b. Vẽ AH vuông góc BD tại H . Tính độ dài đoạn thẳng AH
c. Đường thẳng AH cắt BC và DC lần lượt
tại I và K . Chứng minh 2
AH = HI.HK I B C H A D Hướng dẫn giải a) BD  17cm b) 120 AH cm 17 42 Bài 5:
Cho tam giác ABC vuông tại A . Đường cao A
AH , kẻ EH, HF lần lượt vuông góc với
AB, AC . Chứng minh rằng: 3 a. EB AB       FC AC  B H C b. 3
BC.BE.CF AH Hướng dẫn giải
a) Sử dụng hệ thức giữa cạnh góc vuông với hình chiếu của nó lên cạnh huyền và cạnh huyền
trong các tam giác vuông HBA và HCA
b) Áp dụng hệ thức giữa đường cao và hình chiếu cạnh góc vuông lên cạnh huyền trong tam giác vuông ABC Bài 6:
Cho tam giác ABC cân tại A có AH, BK là D
hai đường cao. Kẻ đường thẳng vuông góc
BC tại B cắt tia CA tại D a. BD  2AH b. 1 1 1   A 2 2 2 BK BC 4HA K B H C Hướng dẫn giải
a) Chứng minh AH là đường trung bình của B ∆ CD
b) Sử dụng hệ thức giữa đường cao và các cạnh góc vuông trong tam giác vuông BCD và áp dụng câu a 43