Tài liệu Toán 9 chủ đề tỉ số lượng giác của góc nhọn

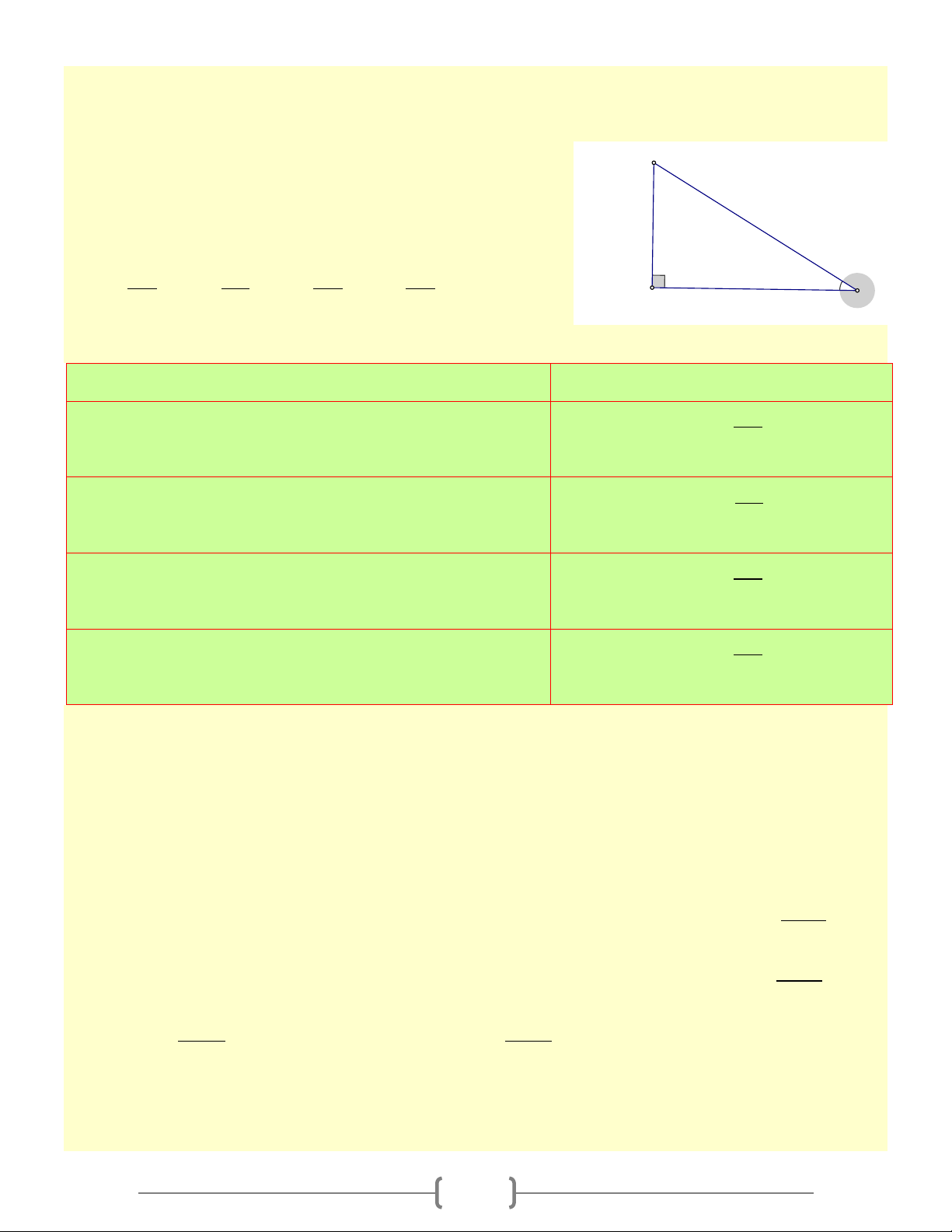
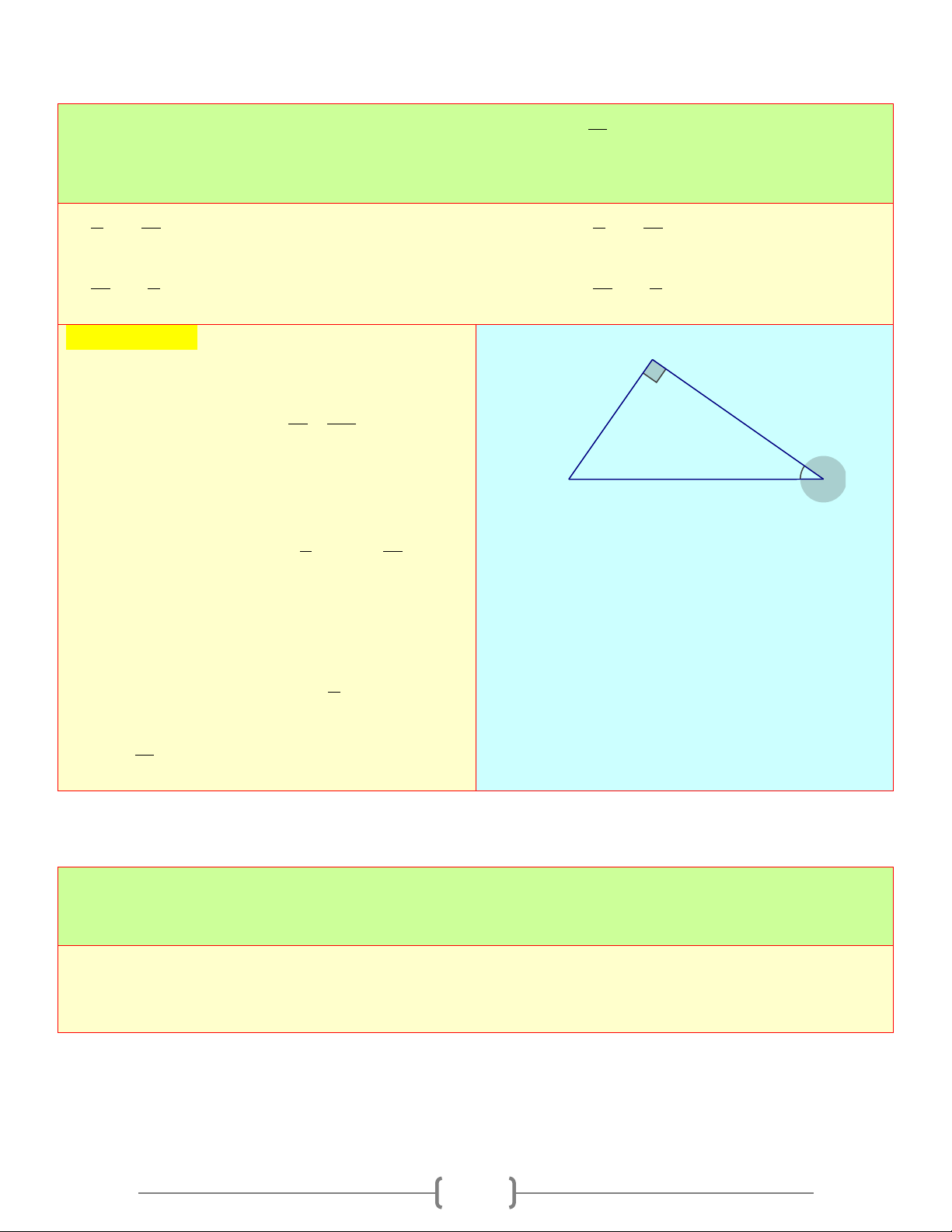
TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN A. Tóm tắt lý thuyết 1. Định nghĩa: B Cho góc nhọn α ( 0 0
0 < α < 90 ) . Dựng A
∆ BC vuông tại A Cạnh huyền sao cho Cạnh đối
α = A ˆBC . Từ đó ta có: AC α = ; AB α = ; AC α = ; BC sin cos tan cotα = α BC BC BC AC A Cạnh kề C Ta có bảng tóm tắt:
Các tỉ số lượng giác của góc nhọn α Công thức
Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin AC sinα = của góc α , kí hiệu BC sinα
Tỉ số giữa cạnh kề và cạnh huyền được gọi là côsin AB cosα = của góc α , kí hiệu BC cosα
Tỉ số giữa cạnh đối và cạnh kề được gọi là tang của AC tanα =
góc α , kí hiệu tanα BC
Tỉ số giữa cạnh kề và cạnh đối được gọi là côtang BC cotα =
của góc α , kí hiệu cotα AC
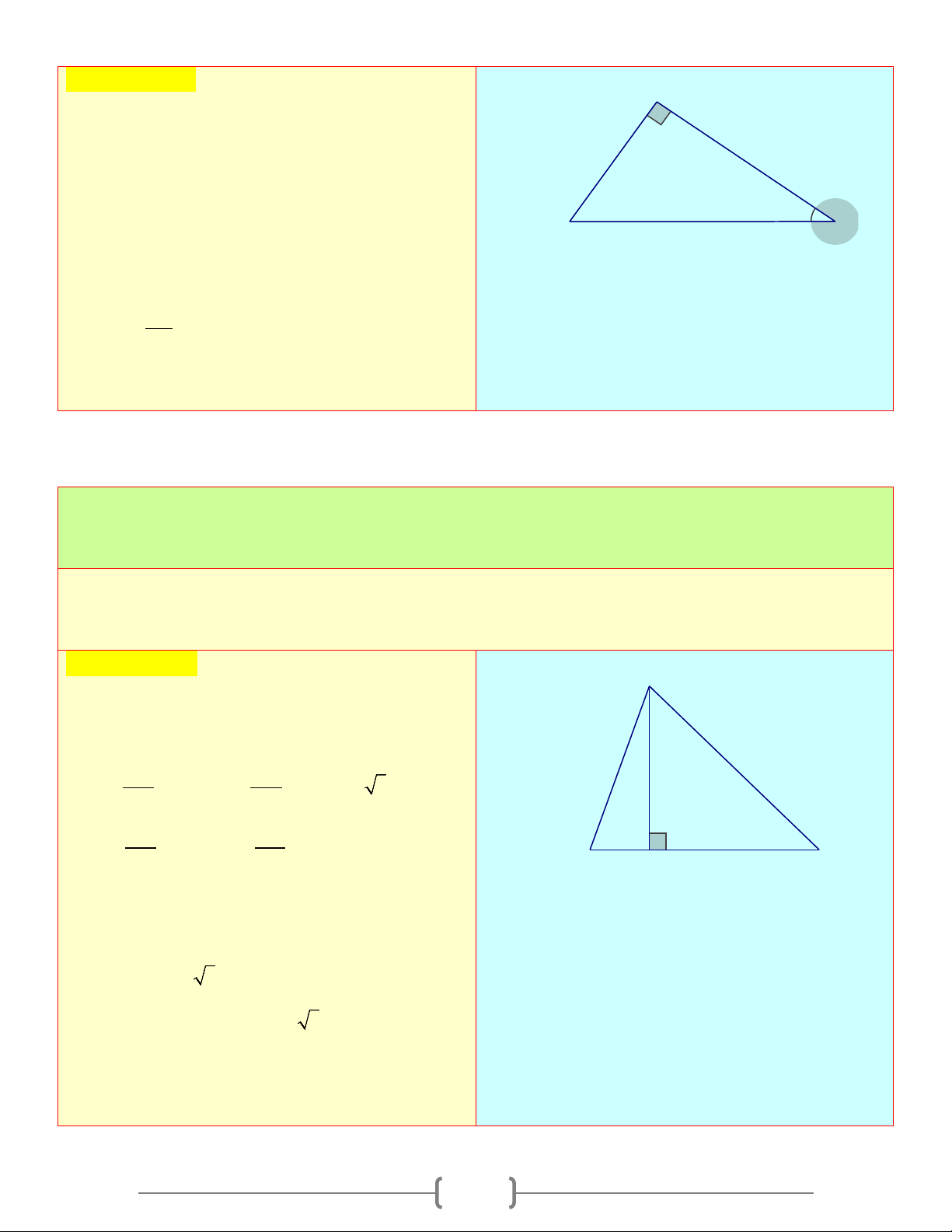
2. Tỉ số lượng giác của hai góc phụ nhau
Định lí: Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia Cụ thể ta có: Nếu 0
α + β = 90 thì Sinα=Cosβ;Cosα=Sinβ;tanα=cotβ;tanβ =cotα
3. Một số hệ thức liên hệ giữa các tỉ số lượng giác +) Sinα ≤1 +) Cosα ≤1 +) α tan Sin α = Cosα +) tanα.Cotα =1 +) α 2 2
Sin α + Cos α =1 +) Cos Cotα = Sinα +) 2 1 1+ tan α = +) 2 1 1+ Cot α = 2 cos α 2 Sin α 1
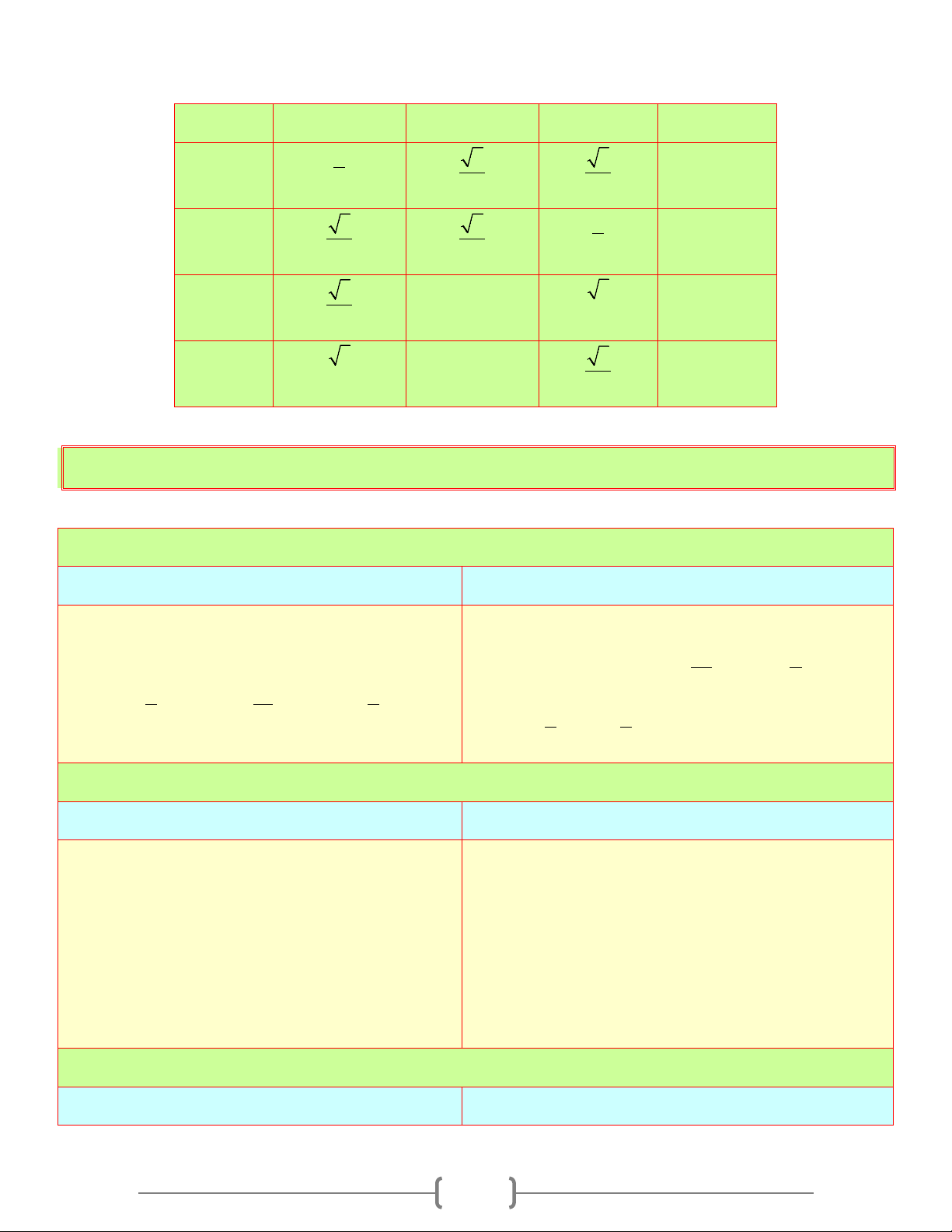
4. Bảng tỷ số lượng giác của một số góc đặc biệt 0 30 0 45 0 60 0 90 Sinα 1 2 2 3 1 2 2 cosα 3 1 2 0 2 2 2 tanα 3 1 3  3 cotα 3 1 3 0 3
B. Bài tập và các dạng toán
Dạng 1: Tính tỉ số lượng giác của góc nhọn, tính cạnh, tính góc
Cách giải: Sử dụng các kiến thức trong phần tóm tắt lý thuyết Bài 1: Đề bài Lời giải
Tìm các tỉ số lượng giác còn lại của góc α, Ta có: biết: 2 2 2 16 4
Sin α + cos α =1⇒ cos α =
⇒ cosα = (cosα > 0) 25 5 a. 3 Sinα = b. 12 cosα = c. 4 tanα = 5 13 3 3 4
⇒ tanα = ;cotα = 4 3 Bài 2: Đề bài Lời giải Tìm góc nhọn α, biết: a) Ta có:
a. sinα = cosα sinα = c os α
⇒ sinα = sin( 0 90 −α )
b. tanα = cotα 0 0 ⇔ α = 90 −α ⇒ α = 45
b) Ta có: tanα = cotα ⇒ tanα = tan( 0 90 −α ) 0 0 ⇔ α = 90 −α ⇒ α = 45 Bài 3: Đề bài Lời giải 2
Tính giá trị của các biểu thức sau 2 2 a) Ta có:  2   1 A 4   2.  = − + −     3 =1 a. 2 0 2 0 3 0
A = 4 − sin 45 + 2cos 60 − 3cot 45  2   2  b. 0 0 0
B = tan45 .cos30 .cot30 b) Ta có: 3 3 B =1. . 3 = c. 2 0 2 0 2 0
C = cos 15 + cos 25 +...+ cos 75 2 2 d. 2 0 2 0 2 0
D = sin 10 + sin 20 +...+ sin 80 c) Ta có: C = ( 2 0 2 0 cos + cos ) 2 0 15 75 +...+ cos 45 2  2  7 = 1+1+1+   =  2  2   d) Ta có: D = ( 2 0 2 0 sin + cos )+ +( 2 0 2 0 10 10
... sin 40 + cos 40 ) = 1+1+1+1 = 4 Bài 4:
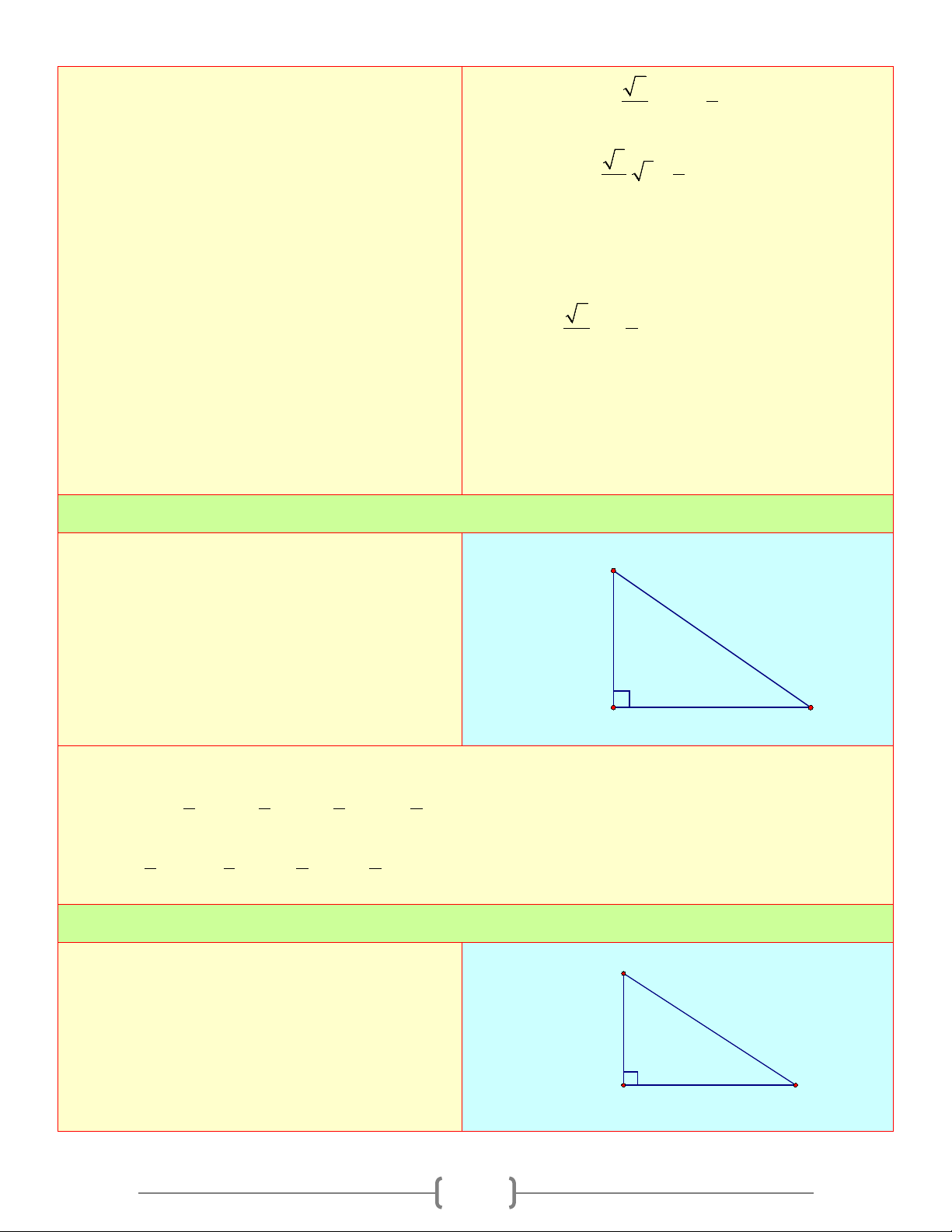
Cho tam giác ABC vuông tại C có A BC =1,2c ;
m AC = 0,9cm . Tính các tỉ số lượng
giác của góc B , từ đó suy ra tỉ số lượng giác của góc 0,9 A C 1,2 B Lời giải Ta có: 3 4 3 4
SinB = ;cosB = ;tanB = ;CotB = 5 5 4 3 4 3 4 3
⇒ SinA = ;CosA = ;tanA = ;cotA = 5 5 3 4 Bài 5:
Cho tam giác ABC vuông tại A có C AB =1,6c ;
m AC =1,2cm . Tính các tỉ số lượng
giác của góc B , từ đó suy ra tỉ số lượng 1,2 giác của góc C . A 1,6 B 3 Lời giải Ta có: 3 4 3 4
SinB = ;cosB = ;tanB = ;cotB = 5 5 4 3 4 3 4 3
⇒ SinC = ;CosC = ;tanC = ;cotC = 5 5 3 4 Bài 6:
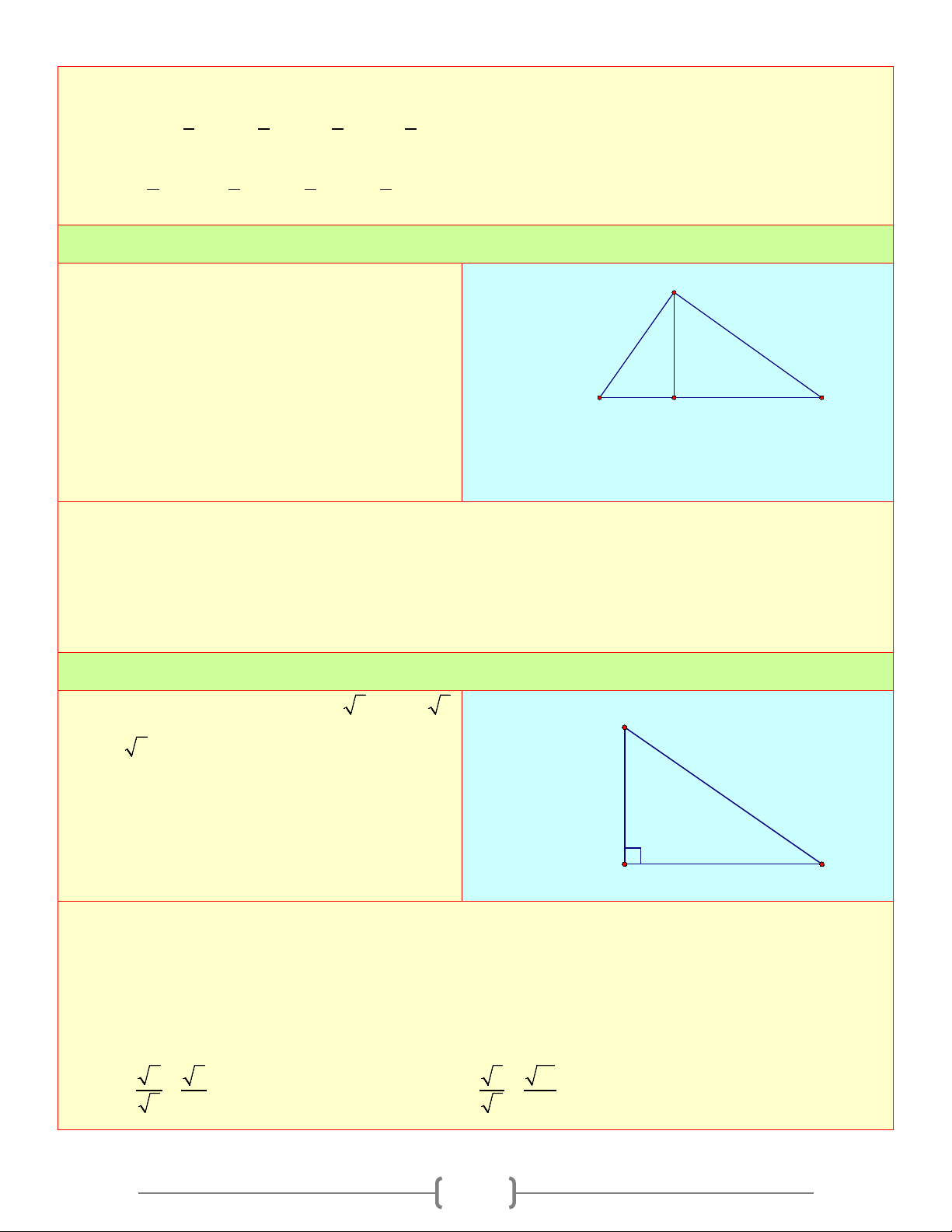
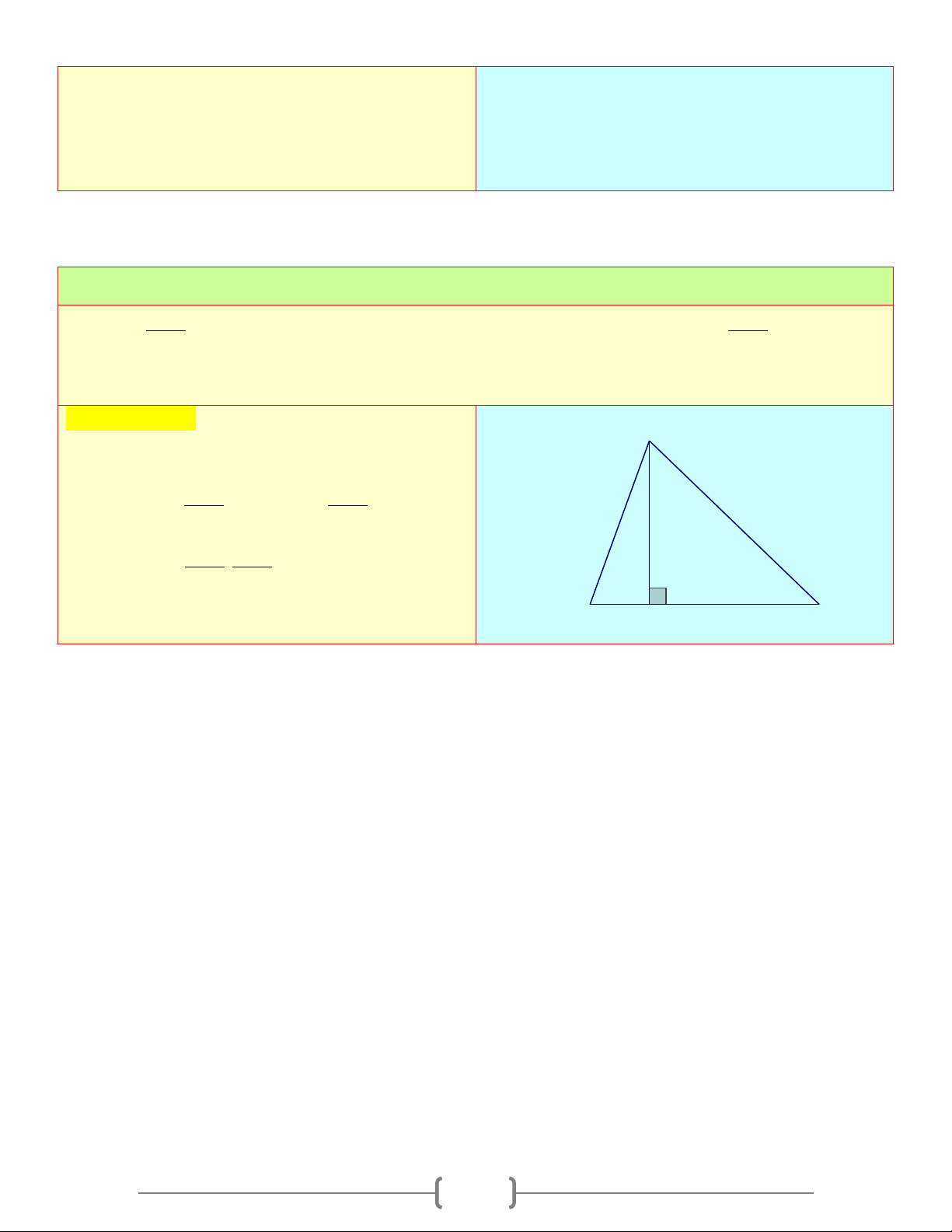
Cho tam giác ABC vuông tại A , đường cao A
AH (H ∈ BC) , hãy tính sinB và sinC làm 13
tròn kết quả đến chữ số thập phân thứ tư
trong các trường hợp sau 4 3 C H 5 B a) AB =13 , m BH = 0,5dm b) BH = 3c , m CH = 4cm Lời giải
a) Áp dụng các tỉ số lượng giác cho tam giác vuông ABH để tính sinB , rồi từ đó suy ra sinC
b) Áp dụng hệ thức lượng về cạnh góc vuông và hình chiếu lên cạnh huyền trong tam giác
vuông ABC để tính AB . Sau đó làm tương tự câu a Bài 7:
Cho tam giác ABC có AB = a 5, BC = a 3 A AC = a 2
a) Chứng minh tam giác ABC vuông
b) Tính các tỉ số lượng giác của góc B , từ
đó suy ra các tỉ số lượng giác của góc A C B Lời giải
a) Dùng định lý pytago đảo, ta có: 2 2 2
AB = AC + BC ( 2 2 2
5a = 3a + 2a ) ⇒ A
∆ BC vuông tại C b) Tính được: - 2 6 SinB = = - 3 15 cos B = = 5 5 5 5 4 - 2 6 tan B = = - 3 3 6 CotB = = 3 3 6 6 Bài 8:
Cho tam giác ABC vuông tại A , AB = 5cm , A 5
cotB = . Tính độ dài các đoạn thẳng AC và 8 BC
a) Chứng minh tam giác ABC vuông B C
b) Tính các tỉ số lượng giác của góc B , từ
đó suy ra các tỉ số lượng giác của góc A Lời giải
Áp dụng tỉ số cotB trong tam giác vuông ABC và định lý pytago ta tính được AC = 8c , m BC = 89cm Bài 9:
Cho tam giác ABC vuông tại A , A 5 AB = 6c , m tanB =
. Hãy tính độ dài đường 12 M 6
cao AH và trung tuyến BM của tam giác ABC B H C Xét ∆  ABH (H ) 30 601 ⇒ AH = (cm); BM = (cm) 13 4 Bài 10:
Cho tam giác ABC vuông tại C , có A BC =1,2c ;
m AC = 0,9cm . Tính các tỉ số lượng
giác của góc B . Từ đó suy ra tỉ số lượng 0,9 giác của góc A B 1,2 C Ta có: 3 4 3 4 4 3 4 3
sinB = ;cosB = ;tanB = ;cotB = ⇒ sinA = ;cosA = ;tanA = ;cotA = 5 5 4 3 5 5 3 4 5 Bài 11:
Cho tam giác ABC vuông tại A , đường cao A
AH (H ∈ BC) biết BH = 4cm , CH =1cm .
Hãy giải tam giác ABC 1 4 C H B
Xét tam giác ABC vuông tại A , áp dụng hệ thức lượng trong tam giác vuông, ta có: +) 2 2
AB = BC.BH ⇒ AB = 20 ⇒ AB = 2 5(cm) ⇒ AC = 5(cm) +) Ta có: AC 5 1 = = = ⇒  0 =  AB = = ⇒  0 tanB B 45 ;tanC 2 C = 45 AB 2 5 2 AC Bài 12:
Cho tam giác ABC vuông tại A , đường cao A
AH (H ∈ BC) , biết BH = 4cm , AC = 3 13cm . 3 13
Hãy giải tam giác ABC 4 C H B
Đặt HC = x(cm)
Áp dụng hệ thức lượng trong tam giác vuông ABC , ta có: x = 9(tm) 2 2 2
AC = BC.CH = (4 + x).x ⇒ x + 4x = 9.13 ⇒ x + 4x + 4 =121⇒  x = 1 − 3(loai)
Ta có: BC = BH + HC =13(cm) +) 2
AB = BH.BC =13.4 = 52 ⇒ AB = 2 13(cm) +)  AC 3 13 3 = = = ⇒  0 = ⇒  0 SinB B 56 C = 34 BC 13 13 Bài 13:
Cho tam giác ABC vuông tại A , có: A AB =10c , m AC =15cm I a. Tính góc B 15 10 H
b. Phân giác trong của góc B cắt AC tại I . Tính AI B C 6
c. Vẽ AH vuông góc với BI tại H . Tính AH
a) Xét tam giác ABC vuông tại A , áp dụng hệ thức lượng trong tam giác vuông, ta có:  AC 15 3 = = = ⇒  0 tanB B = 56 AB 10 2 b) Ta có:  AI = ⇒ =  0 tanABI AI A .
B tanABI =10.tan28 = 5,3(cm) AB c)  AH 0 SinABH = ⇒ AH = A .
B Sin28 = 4,7(cm) AB Bài 14:
Cho tam giác ABC vuông tại A , đường cao A
AH = 6cm(H ∈ BC), biết  2 tanC = . Hãy tính 3
độ dài các cạnh: HB, HC, AB, AC 6 B H C Lời giải
Theo giả thiết ta có:  2 AH 2 tanC = ⇒ = 3 CH 3 Lại có: AH HB AB 2 H .2 A 6.2 AH.3 A ∆ HB# C ∆ ( HA g.g) ⇒ = = = ⇒ HB = = = 4;CH = = 9 CH HA AC 3 3 3 2
Xét tam giác ABC vuông tại A, áp dụng hệ thức lượng trong tam giác vuông ta có: 2 2
AB = BH.HC ⇔ AB = 2 13(cm); AC = CH.CB ⇔ AC = 3 13(cm) 7 Bài 15:
Cho tam giác ABC vuông tại A , có A =  0 AC 15c ,
m B = 50 . Hãy tính độ dài a) AB, AC D 15 b) phân giác CD 500 B a C Lời giải
a) Tam giác ABC vuông ở A , theo hệ thức lượng về cạnh và góc trong tam giác vuông, ta có: =  0
AB AC.cotB =15.cot50 ≈15.0,8391 ≈12,59(cm) =  AC 15 15
AC BC.sinB ⇒ BC = = ≈ ≈19,58 cm 0 ( )  sinB si 50 n 0,7660
b) Tam giác ABC vuông ở A nên:  +  0 = ⇒  0 = −  0 B C 90 C 90 B = 40
CD là tia phân giác của C , ta có:  1 =  1 0 0 ACD C = .40 = 20 2 2
Trong tam giác vuông ACD vuông tại A , theo hệ thức lượng về cạnh và góc ta có: =  0 AC 15 AC C . D cosAC . D cos20 ⇒ CD = = ≈ 15,96 cm . 0 ( ) cos20 0,9397 Bài 16: Cho tam giác ABC nhọn, có A
BC = a, AC = b, AB = c Chứng minh rằng: 2 2 2 = + −  a b c 2 . bc cosA H B C Lời giải
Vẽ đường cao CH của tam giác ABC HA ∆
C vuông tại H nên:  AH = ⇒ =  cosA AH AC.cosA AC HA ∆
C vuông tại H , theo định lý Pytago ta có: 2 2 2
AH + HC = AC 8 HB ∆
C vuông tại H , theo định lý Pytago ta có: 2 2 2 = + = ( − )2 2 BC HB HC AB AH + HC 2 2 2 2 2 = − + + = + −  AB 2A . B AH AH AC AC AB 2AC.A . B cosA Vậy 2 2 2 = + −  a b c 2 . bc cosA . 9
BÀI TẬP TRẮC NGHIỆM Câu 1: Cho A
∆ BC vuông tại A . =  AB 6c , m B = α. Biết 5 tanα =
. Độ dài cạnh AC, BC lần lượt 12 là? a) 5 và 13 b) 5 và 2 2 2 2 13 c) 13 và 5 d) 15 và 3 2 2 2 2 Chọn đáp án A A Giải thích: Ta có: a) Trong A ∆ BC có 5 AC tanα = = 12 AB AC = 5t α ⇒  (t > 0) C AB = 12t B Vì 1 5
AB = 6cm ⇒12t = 6 ⇔ t = ⇒ AC = 2 12
b) Áp dụng định lý Pytago vào tam giác vuông A ∆ BC , ta được: 2 2 2 2 2 2  5 BC AB AC BC 6  = + ⇔ = +  2    13 ⇒ BC = (cm)(BC > 0) 2 Câu 2: Cho OP ∆
Q có OQ = 9,6c ,
m PQ =12cm . Số đo các góc của OP ∆
Q lần lượt là? (làm tròn kết quả đến độ) a)  0 =  0 =  0
P 37 ;Q 35 ;O = 37 b)  0 =  0 =  0
P 53 ;Q 37 ;O = 90 c)  0 =  0 =  0
P 90 ;Q 35 ;O = 54 d)  0 =  0 =  0
P 53 ;Q 90 ;O = 37 10 Chọn đáp án B A Giải thích: Ta có: 2 2 OP 
+ OQ = (7,2)2 + (9,6)2 =144( ) 1  2 2 PQ = 12 = 144  (2) α Từ (1)(2), suy ra: 2 2 2
OP + OQ = PQ C B ⇒ OP ∆
Q vuông tại O ⇒  9,6 = = ⇒  0 sinP 0,8 P = 53 1,2  0 = −  0 0 0 Q 90 P = 90 − 53 = 37 Câu 3: Cho A ∆ BC có  0 =  0
B 60 ,C = 45 , AB =10cm . Chu vi của tam giác ABC là? (làm tròn kêt
quả đến chữ số thập phân thứ hai) a) 35,6 b) 35,7 c) 35,8 d) 35,9 Chọn đáp án D A Giải thích: Xét A
∆ HB vuông tại H , ta có:  AH 0 = ⇔ 60 AH sinB sin =
⇒ AH = 5 3 (cm) 10 AB 10  BH 0 = ⇔ 60 BH cosB cos = ⇒ BH = 5(cm) 60° 45° AB 10 B C Xét A
∆ HC vuông tại H , ta có:  0 C = 45 do đó A
∆ HC là tam giác vuông cân tại H
⇒ AH = HC = 5 3 (cm)
Ta có: BC = BH + HC = 5+5 3 =13,65(cm)
Áp dụng định lý Pytago vào tam giác vuông AHC , ta có: 11 2 2 2
AC = AH + HC ⇒ AC ≈12,25(cm) Chu vi tam giác A ∆ BC là: P
= AB + BC + CA = cm ABC 35,9( )
Câu 4: Với góc nhọn α tùy ý. Khẳng định nào sau đây sai a) sinα α tanα = b) cos cotα = cosα sinα
c) tanα.cotα = 2 d) 2 2
sin α + cos α =1 Chọn đáp án C A Giải thích: Ta có: sinα α tanα = và cos cotα = cosα sinα 10 α α ⇒ α. sin α = . cos tan cot =1. cosα sinα 60° 45° B C 12 BÀI TẬP VỀ NHÀ Bài 1:
Cho tam giác ABC vuông tại A có A AB = 60m ;
m AC = 8cm . Tính các tỉ số lượng
giác của góc B Từ đó suy ra tỉ số lượng 6 8 giác của góc C B C Lời giải Ta có: 8 4 6 3 8 4 3 sinB = = ;cosB =
= ;tanB = = ;cotB = 10 5 10 5 6 3 4 3 4 3 4
⇒ sinC = ;cosB = ;tanB = ;cotB = . 5 5 4 3 Bài 2:
Cho tam giác ABC vuông tại A . Hãy tính A
các tỉ số lượng giác của góc C biết rằng cosB = 0,6 B C Lời giải Ta có: 2 2 2 2 2 + = ⇒ + = ⇒ = ⇒  ⇒  Sin B cos B 1 Sin B 0,6 1 Sin B 0,074 B C Bài 3:
Cho tam giác ABC vuông tại A . Biết A AB = 30cm ,  5 B = α,tanα = . Tính BC, AC 12 30 B C Lời giải Ta có: 13  5 AC 5 AC 5 150 B = α,tanα = ⇒ = ⇒ = ⇒ AC = = 12,5 ⇒ BC 12 AB 12 30 12 12 Bài 4:
Cho tam giác ABC vuông tại A , đường cao A
AH . Tính sinB, sinC a) AB =13c , m BH = 5cm b) BH = 3c , m CH = 4cm B H C Lời giải
a) Ta có: AB =13c ,
m BH = 5cm ⇒ AH ⇒ BC ⇒ SinB, SinC
b) Ta có: BH = 3c ,
m CH = 4cm ⇒ AH ⇒ AB, AC ⇒ SinB, SinC Bài 5:
Cho tam giác ABC vuông tại A , góc  0 C = 30 BC =10cm B
a. Tính AB, AC b. Kẻ từ N
A các đường thẳng AM , AN lần
lượt vuông góc với các đường phân giác M
trong và ngoài của góc B . Chứng minh A C MN = AB
c. Chứng minh các tam giác MAB và ABC
đồng dạng. Tìm tỉ số đồng dạng. Lời giải
b) Chú ý: Hai đường phân giá của hai góc kề bù vuông góc với nhau
c) Ta có: BM là phân giác của góc B . Từ đó tính được số đo các góc của tam giác MAB
*) Chú ý: Tam giác MAB và ABC đều là các tam giác nửa đều, từ đó tính được tỉ số đồng dạng là 0,5. 14 Bài 6:
Cho tam giác ABC vuông tại A( AB < AC), B  0
C = α < 45 , đường trung tuyến AM , đường H
cao AH , MA = MB = MC = a . Chứng minh M rằng:
a) sin2α = 2sinα.cosα A C b) 2
1+ cos2α = 2cos α c) 2
1− cos2α = 2sin α a) Ta có:  AH 2AH 2AH A . = 2α; 2α = = = = 2. B AC AMH Sin = 2.sinα.cosα 2 AM 2AM BC BC 2 b) HM HC 2HC AC 2 1+ cos2α =1+ = = = 2. = 2.cos α 2 AM AM BC BC 2 c) HM HB 2HB AB 2 1− cos2α =1− = = 2. == 2.sin α 2 AM AM BC BC 15